Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 119
Você abre a torneira da cozinha muito lentamento, de modo que um filete de água escoa para a pia. Você nota que o escoamento é laminar e que isso se reforça para os primeiros 50 mm de descida. Para medir a vazão, você leva três minutos para encher uma garrafa de 1 L, e você estima que o filete de água tem 5 mm de diâmetro. Considerando que a velocidade em qualquer seção transversal seja uniforme e desprezando os efeitos viscosos, deduza expressões e construa um gráico para as variações da velocidade da corrente e do diâmetro como função de (adote a origem de coordenadas na saída da torneira). Qual a velocidade e o diâmetro do filete 50 mm abaixo desse ponto?
Passo 1
Tá legal, vamos começar o exercício calculando a vazão do sistema:
Agora conseguimos calcular a velocidade na saída da torneira:
Passo 2
Agora vamos aplicar Bernoulli entre os pontos de saída da torneira (0) e qualquer ponto longe da saída:
Isolando temos:
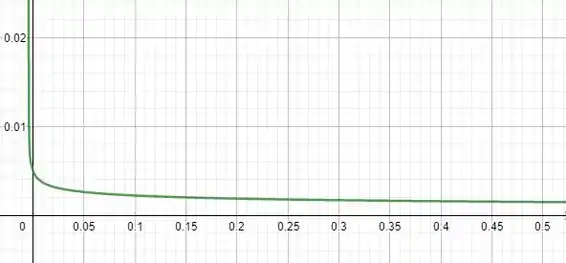
A velocidade do filete para é:
O gráfico que representa a velocidade em função da distância é:
Passo 3
Agora, para obter uma expressão para o diâmetro em função de , podemos usar a conservação da massa no sistema entre os pontos de saída da torneira e um ponto qualquer mais distante:
Agora, substituindo a expressão para a velocidade encontrada no passo 2, temos:
E o diâmetro após 50 mm de descida será:
O gráfico que representa o diâmetro em função de é:
