Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 87
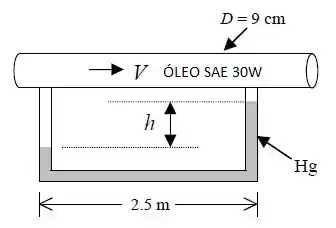
Óleo SAE 30W a 20°C escoa por um tubo de 9 cm de diâmetro na figura abaixo a uma velocidade média de 4,3 m/s. (a) Verifique se o escoamento é laminar. (b) Determine a vazão volumétrica em m³/h. (c) Calcule a leitura h esperada no manômetro de mercúrio, em cm.
Passo 1
Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos?
(a) Vamos checar o número de Reynolds pra essa belezinha!!! Bem, primeiro precisamos então pegar as propriedades do óleo nas condições dadas do enunciado, ou seja, a 20°C. Vamos usar o Apêndice A.3 do livro.
Passo 2
(b) A velocidade média é conhecida, então é moleza calcular a vazão volumétrica pedida, se liga!!
Passo 3
(c) Como estamos em um escoamento laminar em um tubo, podemos usar a equação de Poiseuille que relaciona a queda de pressão com a vazão!!!
Olha que belezura, a gente sabe que a diferença de pressão pode ser calculada pela hidrostática, uma vez que na mesma altura, temos a mesma pressão!!