Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 98

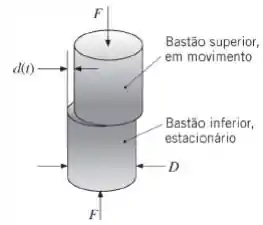
Juntas de alta qualidade podem ser formadas com solda por fricção. Considere a solda por fricção de dois bastões de Inconel com 40   m m de diâmetro. O bastão inferior encontra-se estacionário, enquanto o superior é forçado em um movimento linear de vai e volta caracterizado por um deslocamento horizontal instantâneo, d ( t )   =   a   c o s ( ω t ) , sendo a   =   2   m m e   ω   =   1000   r a d / s . O coeficiente de atrito de deslizamento entre as duas peças é μ   =   0,3 . Determine a força de compressão que deve ser aplicada para aquecer a junta até o ponto de fusão do Inconel em t   =   3   s , partindo de uma temperatura inicial de 20 ° C . Sugestão: A frequência do movimento e a taxa de aquecimento resultante são muito altas. A resposta da temperatura pode ser aproximada como se a taxa de aquecimento fosse constante no tempo, igual ao seu valor médio.

Passo 1

Aqui nós temos o diâmetro e a temperatura inicial de duas barras de Inconel, nas quais suas propriedades vão ser retiradas da Tabela A.1. Além disso, temos também a amplitude, frequência de movimento da haste superior e o coeficiente de fricção.

Com isso, precisamos encontrar a força de compressão necessária para levar a haste ao ponto de fusão em 3 segundos. Então vamos as nossas considerações!

Passo 2

Para resolver essa questão vamos assumir que:

(1) A perda de calor nas superfícies das hastes é desprezível;

(2) As hastes são efetivamente semi-infinitas;

(3) A geração de calor por atrito pode ser tratada como constante no tempo;

(4) As propriedades são constantes.

Nós vamos começar expressando o fluxo de calor por atrito em termos da força compressiva desconhecida, F n .

q ' ' = - F t → ∙ V → A = μ F n V A = μ F n A d d d t = μ F n A a ω   sen ⁡ ω t

Na equação acima, foi utilizado o fato de que a força de atrito sempre se opõe à direção do movimento, então,

F t → ∙ V → = - F t V

O valor médio do fluxo de calor é encontrado através da integração em um período de   sen ⁡ ω t , ou seja, π / ω   :

q s ' ' - = ω π ∫ 0 π ω μ F n a ω A   sen ⁡ ω t d t = - 1 π μ F n a ω A cos ⁡ ω t 0 π ω

q s ' ' - = 2 μ F n a ω π A

Onde,

A = π D 2 2

Porque o calor é conduzido nas duas direções

Passo 3

Podemos encontrar a temperatura da superfície para a distribuição de temperatura em um sólido semi-infinito com fluxo uniforme de calor na superfície. Avaliando em x   =   0 temos:

T s - T i = 2 q s ' ' - α t π 1 2 k

Com T s igual à temperatura de fusão, podemos resolver para q s ' ' - :

q s ' ' - = k T s - T i 2   π α t 1 2

Substituindo os valores,

q s ' ' - = 23,6 W m . K 1665   K - 293   K 2   π 4,49 × 10 - 6 m 2 / s   ×   3 s 1 2

q s ' ' - = 7,82 × 10 6   W / m 2

Então podemos resolver para F n :

F n = q s ' ' - π A 2 μ a ω = 7,82 × 10 6 W m 2 × π × p i   0,04   m 2 / 2 2 × 0,3 × 0,002   m × 1000   r a d / s = 51,4   k N

F n = 51,4   k N

Resposta

F n = 51,4   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma parede plana, que tem um de seus lados ( x=0 ) termicamente isolado, está inicialmente a uma temperatura uniforme T i , quando sua superfície exposta em x=L tem a sua temperatura subitamente eleva
Uma lâmina espessa de aço (ρ = 7800 kg/m³, c = 480 J/(kg · K), k = 50 W/(m · K)) está inicialmente a 300 °C e é resfriada por jatos de água colidindo sobre uma de suas superfícies. A temperatura da ág
Dois grandes blocos feitos com materiais diferentes, como cobre e concreto, ficaram em repouso no interior de uma sala (23°C) por um longo período de tempo. Qual dos dois blocos, se algum, parecerá ma
Uma pavimentação de asfalto, em um dia quente de verão, pode atingir temperaturas tão elevadas quando 50°C. Suponha que tal temperatura esteja presente ao longo da espessura de um pavimento quando, de
Uma parede plana de espessura 0,6 m (L = 0,3 m) é feita de aço (k = 30 W/(m · K), ρ = 7900 kg/m³, c = 640 J/(kg · K)). Ela está inicialmente a uma temperatura uniforme e é, então, exposta ao ar em sua