Enunciado
Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 116
Uma parede, com de espessura e difusividade térmica de , encontra-se inicialmente a uma temperatura uniforme igual a . Subitamente, uma de suas faces tem a sua temperatura reduzida a , enquanto a outra é perfeitamente isolada.
(a) Usando a técnica explícita de diferenças finitas, com incrementos espacial e no tempo de e , respectivamente, determine a distribuição de temperaturas em .
(b) Com e , calcule para , sendo o tempo necessário para que a temperatura em cada um dos pontos nodais atinja um valor que se encontre a menos de do seu valor em regime estacionário. Repita os cálculos anteriores para . Para cada valor de , represente graficamente os históricos das temperaturas em cada face da parede e no seu plano central.
Passo 1
Nessa questão nós temos uma parede de de espessura, com difusividade térmica , inicialmente a uma temperatura uniforme de , com uma face repentinamente abaixada para enquanto a outra face está perfeitamente isolada.
A partir disso queremos a distribuição de temperatura na parede minutos após a mudança na temperatura da superfície e o efeito de nos históricos de temperatura das superfícies e no plano médio.
Passo 2
Para resolver essa questão vamos assumir que a condução transitória é unidimensional e as propriedades são constantes.
As equações de diferença finita para os pontos interiores, nós e , podem ser determinadas a partir de:
Com,
Observe que o critério de estabilidade , é atendido. Portanto, combinando as equações anteriores temos,
para m =
Passo 3
A distribuição de temperatura também pode ser determinada a partir da aproximação de um termo da solução exata. A superfície isolada é equivalente ao plano médio de uma parede de espessura . Portanto,
E,
Da Tabela 5.1, . Então:
Ou,
Este valor mostra uma excelente concordância com para o método das diferenças finitas.
Passo 4
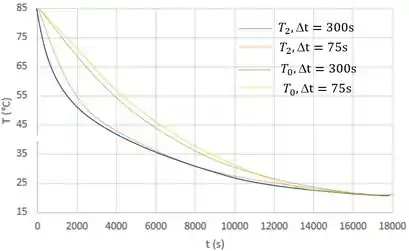
Para a letra (b) queremos representar graficamente os históricos das temperaturas em cada face da parede e no seu plano central. Onde temos:
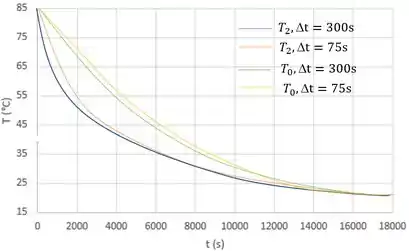
Além de pequenas diferenças durante os estágios iniciais do transitório, há uma excelente concordância entre os resultados obtidos para as duas etapas de tempo. A queda de temperatura na superfície isolada deve ficar abaixo da do plano intermediário.
Resposta
