Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 23
Uma lâmina de aço, com espessura , é temperada pela sua passagem através de um grande forno cujas paredes são mantidas a uma temperatura , que corresponde a dos gases de combustão que escoam através do forno . A lâmina, cuja massa específica, calor específico, condutividade térmica e emissividade são , e ; respectivamente, deve ser aquecida de a .
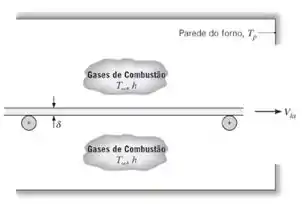
(a)Para um coeficiente de transferência de calor uniforme e uma temperatura , determine o tempo necessário para aquecer a lâmina. Se a lâmina se move a uma velocidade de ; qual deve ser o comprimento do forno?
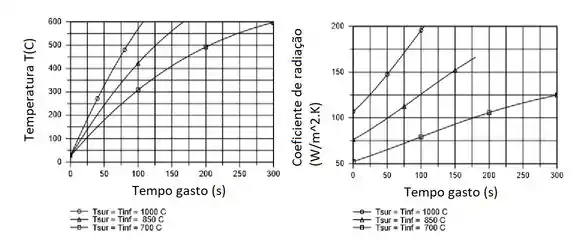
(b)O processo de têmpera pode ser acelerado (a velocidade da lâmina aumentada) pelo aumento da temperatura ambiente. Para o comprimento do forno obtido na parte (a), determine a velocidade da lâmina para e para . Para cada conjunto de temperaturas ambiente (), represente graficamente a temperatura da lâmina em função do tempo na faixa . Ao longo dessa faixa, represente também o coeficiente de transferência de calor por radiação, , como uma função do tempo.
Passo 1
Here we go! (a)Considerando uma massa fixa (de controle) da tira móvel, sua variação de temperatura com o tempo pode ser obtida a partir de um balanço energético que iguala a mudança no armazenamento de energia à transferência de calor por convecção e radiação. Não entendeu? Se ainda não, vou falar de áreas: Se a área de superfície associada a um lado da massa de controle for designada como e na Equação 5.15, o que reduz para
Ou, introduzindo o coeficiente de radiação das Equações 1.8 e 1.9 e integrando:
Passo 2
Então pessoal, aqui temos dois caminhos: integrar esse monstro para achar uma aproximação, ou trabalhar numericamente, que pra esse conteúdo eu julgo o mais adequado, considerando que questões desse tipo, sempre é bom termos valores numéricos até mesmo para comparação com a vida real. Portanto, utilizando valores numéricos com , encontramos corresponde a:
Neste caso, o comprimento do forno necessário é
Passo 3
(b) Para e , a integral numérica é aproximadamente e , respectivamente. Portanto, para um , voltamos para a equação lá de cima para calcular as velocidades!
que correspondem a taxas de aumento do processo de e respectivamente. Claramente, a produtividade pode ser aumentada através do aumento da temperatura ambiente do forno, embora às custas do aumento da utilização de energia e dos custos operacionais. Se o processo de recozimento se estende de 25°C (298 K) a 600°C (873 K), a integração numérica produz os seguintes resultados para as temperaturas prescritas para o forno:
