Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 89

Laufer [5] obteve os seguintes dados para média de velocidade próxima à parede no escoamento turbulento completamente desenvolvido de ar em um tubo, para R e U   =   50.000 ( U   =   3   m / s e R   =   123   m m ):

Trace um gráfico com os dados e obtenha a inclinação de melhor ajuste, d u -   / d y . Use isso para estimar a tensão de cisalhamento na parede a partir de τ w   =   μ   d   / d y . Compare o valor estimado com aquele obtido a partir do fator de atrito f calculado com (a) a fórmula de Colebrook (Eq. 8.37) e (b) a correlação de Blasius (Eq. 8.38).

Passo 1

Fala aí galera, vamos para mais um problema de Mecânica dos fluidos. Primeiramente, vamos montar o gráfico:

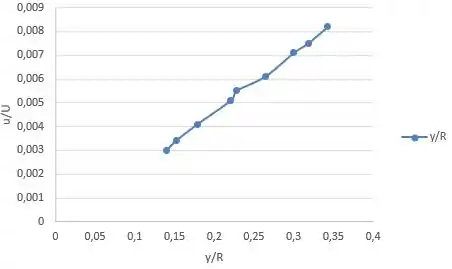
Sabemos que:

d u - U d y R ≈ ∆ u - U ∆ y R = 39,8

d u - d y = U d u - U R d y R = 963 s - 1

Para o ar padrão, μ = 3,72 × 10 - 7 :

τ w = μ d u - d y = 3,58 × 10 - 4

Agora, usando a equação 8.23:

V - U = 2 n 2 n + 1 2 n + 1 = 0,812

Portanto:

R e V = 0,812

R e U = 0,812 × 50000 = 40600

Passo 2

Balanceando as forças em um elemento de fluido infinitesimal:

p + ∆ p π D 2 4 - τ w π D L - p π D 2 4 = 0

Substituindo e isolando τ w :

τ w = 4,13 × 10 - 4

15% maior.

Resposta

τ w = 3,58 × 10 - 4

τ w = 4,13 × 10 - 4

É 15% maior.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um canudo para refrigerante tem 20 cm de comprimento e 2 mm de diâmetro. Ele fornece refrigerante gelado, aproximado como água a 10°C, à taxa de 3 cm³/s. (a) Qual é a perda de carga através do canudo?
Glicerina a 20°C deve ser bombeada por um tubo liso e horizontal a 3,1 m³/s. Deseja-se que (1) o escoamento seja laminar e (2) a queda de pressão não seja maior que 100 Pa/m. Qual é o diâmetro mínimo
Os tanques de óleo em Pequelândia tem apenas 160 cm de altura e descarregam em um caminhão-pipa por um tubo liso de 4 mm de diâmetro e 55 cm de comprimento. A saída do tubo é aberta à atmosfera, a 145
Dois tanques com água a 20°C são conectados por um tubo capilar de 4 mm de diâmetro e 3,5 m de comprimento. A superfície do tanque 1 está 30 cm acima da superfície do tanque 2. (a) Estime a vazão em m
Óleo SAE 10 a 20°C escoa em um tubo vertical de 2,5 cm de diâmetro. Verifica-se que a pressão é constante em todo o fluido. Qual é a vazão de óleo em m³/h? O escoamento é para cima ou para baixo?