Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 27
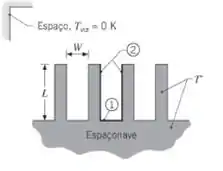
Para melhorar o descarte de calor em espaçonaves, um engenheiro propõe fixar uma série de aletas retangulares à superfície externa da espaçonave e cobrir todas as superfícies com um material que se aproxima de um comportamento de corpo negro. Considere a região em forma de U entre duas aletas adjacentes e subdivida a superfície em componentes associados à base (1) e ao lado (2). Obtenha uma expressão para a taxa, por unidade de comprimento, na qual a radiação é transferida das superfícies para o espaço, que pode ser aproximado por um corpo negro com a temperatura igual ao zero absoluto. As aletas e a base podem ser consideradas isotérmicas a uma temperatura T. Comente os seus resultados. A proposta do engenheiro tem mérito?
Passo 1
Shooow de bolinhas !! Por aqui nós não paramos !!
A questão nos pede para determinar uma expressão para a taxa, por unidade de comprimento, na qual a radiação é transferida das superfícies para o espaço, não é?
Como a superfície (3) recebe radiação das superfícies (1) e (2):
Como:
Então:
E pela reciprocidade:
Então:
Como o somatório da superfície 1 é dada por:
E a área da superfície 1 nós achamos lá na figura:
Então:
Achamos uma das respostas deste problema, não é? Mas não acabamos !!
Passo 2
Também queremos saber se a proposta do engenheiro tem mérito, certo?
Bom, a seção deste problema nos fala que, quando a unidade é mantida a temperatura constante, a emissão é proporcional à área da abertura !!
Como as superfícies (1) e (2) têm a mesma temperatura, o problema pode ser tratado como um gabinete de duas superfícies, que consiste nas superfícies (1), (2) e (3). E, neste caso, nós podemos expressá-lo como:
Agora, quando o comportamento de corpo negro não puder ser alcançado o aprimoramento seria proporcionado pelas aletas !!
E assim nós finalizamos mais umaa !!