Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 38
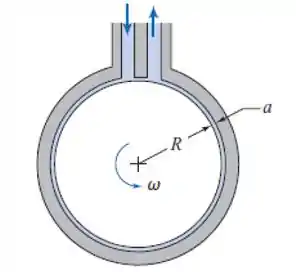
Uma bomba de arrasto viscoso é feita de um invólucro estacionário com um tambor rotativo bem ajustado no seu interior. A folga é pequena comparada com o diâmetro do tambor, de modo que o escoamento no espaço anular entre o invólucro e o tambor pode ser tratado como um escoamento entre placas paralelas. O fluido é arrastado em volta do anel por forças viscosas. Avalie as características de desempenho da bomba de arrasto (diferencial de pressão, potência requerida e eficiência) como funções da vazão volumétrica. Considere que a profundidade normal ao diagrama é .
Passo 1
Tá legal, a primeira coisa que devemos fazer é escrever a equação para a vazão volumétrica para escoamento laminar com gradiente de pressão entre placas estacionárias e paralelas, com a superior se movimentando, essa equação foi dada nessa seção do livro, é a equação 8.9b, dessa forma temos:
Só que, no nosso caso, a velocidade será dada pela rotação do tambor vezes o seu raio, então, temos:
E o gradiente de pressão pode ser dado por:
Então, sabendo que no nosso caso a profundidade normal ao diagrama é , e substituindo essas duas expressões na equação para a vazão, temos:
Então, isolando o gradiente de pressão dessa equação, temos:
Passo 2
Agora, para encontrar uma relação para a potência, nós sabemos que a potência é dada pelo torque vezes a rotação:
Nesse caso, sabemos que o torque é dado pela força vezes o braço de alavanca, que nesse caso é o raio do tambor, então, temos:
E, no nosso caso, a força será dada pela tensão de cisalhamento vezes a área de contato, então, temos:
Agora, nesse caso, precisamos recorrer à tensão de cisalhamento dada pela equação 8.9a:
No nosso caso, estamos interessados na potência, que é calculada com o raio máximo do tambor, dessa forma, também, precisamos pegar a extremidade do filme, de modo que , assim, substituindo isso na equação acima, além das expressões vistas no passo 1 para e o gradiente de pressão, então, temos:
Então, substituindo essa expressão na equação para o torque, temos:
Agora, substituindo a expressão para encontrado no passo 1, temos:
Então, substituindo essa expressão na equação para a potência, temos:
Passo 3
E, por fim, para encontrar a expressão para a eficiência, sabemos que a potência produzida pode ser dada pela vazão vezes o gradiente de pressão:
Substituindo a expressão encontrada para , temos:
Então, a eficiência será dada pela potência de saída pela potência de entrada, dada pela expressão encontrada no passo 2, então, teremos: