Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 37
Microcomponentes eletrônicos (microchips) são suportados por uma fina película de ar sobre uma superfície horizontal durante um estágio do processo de fabricação. Os “chips” têm 11,7 mm de comprimento, 9,35 mm de largura e massa de 0,325 g. O filme de ar tem 0,125 mm de espessura. A velocidade inicial de um chip é ; a velocidade do chips diminui como resultado do atrito viscoso no filme de ar. Analise o movimento do chip durante a desaceleração de modo a desenvolver uma equação diferencial para a velocidade do chip como uma função do tempo . Calcule o tempo requerido para o chip perder 5% da sua velocidade inicial. Esboce a variação da velocidade do chip versus o tempo durante a desaceleração. Explique porque o perfil de variação de velocidade aparenta a forma que você esboçou.
Passo 1
Tá legal, a primeira coisa que devemos fazer é escrever a equação para a tensão de cisalhamento entre o chip e a superfície:
E, nesse caso, como o chip se move e a superfície está em repouso, então vamos considerar o perfil de velocidade como sendo linear, dessa forma, teremos:
Em que é a espessura do filme. Desse modo, a equação para o cisalhamento se torna:
Agora, sabemos que a força de cisalhamento será o produto da tensão de cisalhamento pela área de contato, dada por:
E, substituindo a expressão para nessa equação, temos:
Passo 2
Então, agora, vamos aplicar a equação do equilíbrio de forças na direção para o chip, tendo só a força de atrito, a equação se torna:
Então, substituindo a expressão encontrada no passo 1 para a força de atrito, temos:
Separando as variáveis, temos:
Agora vamos integrar essa expressão dos dois lados:
Pela propriedade da subtração dos logarítmos, podemos escrever:
Passo 3
Agora, vamos substituir os valores dados no enunciado na equação obtida no passo 2 para obter o tempo requerido para o chip perder 5% da sua velocidade inicial, ou seja, para que , então, a equação se torna:
Passo 4
Agora, retomando a equação do passo 2, podemos isolar a velocidade e deixar ela em função do tempo, de forma que teremos:
E o gráfico dessa função será:
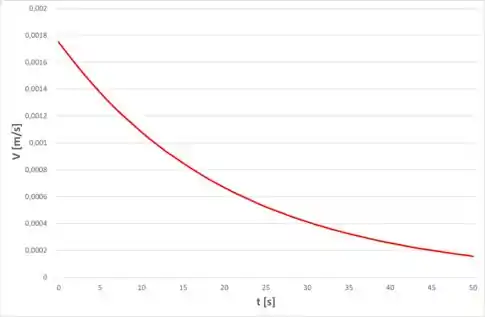
Podemos ver que o decaimento de velocidade é maior no começo, justamente porque a variação da velocidade depende da própria velocidade, pois ela está diretamente ligada ao módulo da força de atrito gerado.