Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 32
Considere o escoamento completamente desenvolvido entre placas paralelas, com a placa superior movendo a ; o espaçamento entre as placas é . Determine a vazão em volume por unidade de profundidade para o caso de gradiente de pressão zero. Se o fluido for ar, avalie a tensão de cisalhamento sobre a placa inferior e trace a distribuição de tensão de cisalhamento através do canal para o caso de gradiente de pressão zero. A vazão aumentará ou diminuirá, se o gradiente de pressão for adverso? Determine o gradiente de pressão que dará tensão de cisalhamento zero em . Trace o gráfico da distribuição de tensão de cisalhamento em uma seção do canal para o último caso.
Passo 1
Tá legal! A primeira coisa que devemos fazer é escrever a equação para o perfil de velocidade nesse caso, que será dado pela equação 8.8 vista nessa seção do livro, então, teremos:
Então para um gradiente de pressão , temos:
Agora, escrevendo a equação da vazão volumétrica, temos:
Deixando a vazão no formato pedido, ou seja, por unidade de profundidade, temos:
Substituindo a expressão para acima, temos:
Integrando essa expressão, temos:
Substituindo os limites de integração, ficamos com:
Substituindo os valores conhecidos, temos:
Passo 2
Agora, sabemos que a tensão de cisalhamento é dada por:
Então, derivando a expressão da velocidade para o gradiente de pressão zero encontrado no passo 1, temos:
Dessa forma, substituindo esse valor na expressão para , temos:
Substituindo os valores conhecidos (lembrando de pegar o dado para a viscosidade do apêndice A), temos:
Então, a tensão de cisalhamento será constante. Agora, se o gradiente de pressão por positivo, então a vazão diminuirá, mas, se ele for negativo, então a vazão irá aumentar.
Passo 3
Agora, para o caso onde o gradiente de pressão não é zero, temos a derivada da velocidade como:
Então, dessa forma, a tensão de cisalhamento será:
Então, para o ponto pedido no enunciado, de , temos:
Então, agora, para obter tensão de cisalhamento zero, devemos ter então:
Então, substituindo os valores conhecidos, temos:
Passo 4
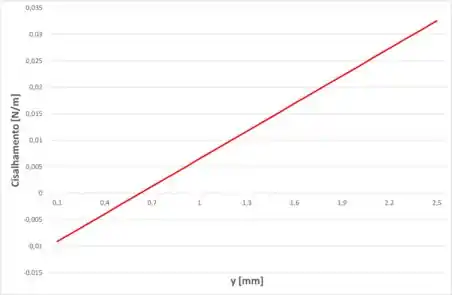
Então, o gráfico da distribuição de tensão de cisalhamento em uma seção do canal para o caso do passo 3 será governado pela equação:
Com o valor de encontrado no passo 3, então, dessa forma, o gráfico será:
