Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 60
A extremidade de um tanque cilíndrico no espaço, que contém um propelente criogênico líquido, deve ser protegida da radiação externa (solar) pela colocação de uma fina barreira metálica em frente ao tanque. Considere que o fator de forma Ftb entre o tanque e a barreira seja igual à unidade, que todas as superfícies são difusas e cinzas, e que a vizinhança está a 0 K.
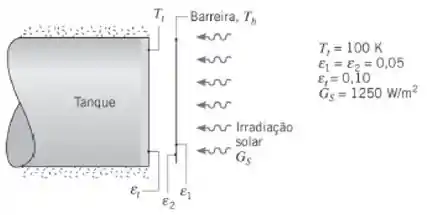
Determine a temperatura da barreira Tb e o fluxo térmico (W/m2) para a extremidade do tanque.
Passo 1
Vamos lá! A gente tem um tanque no espaço e estamos protegendo ele da radiação solar usando uma barreira!
Queremos descobrir a tempertura da barreira e o fluxo térmico, entre a superfície da barreira e o tanque!
Considerando que o fator de forma , podemos começar escrevendo :
Temos duas icógnitas que não conhecemos, e , então precisamos de uma outra equação! Vamos fazer um esqueminha do que esta acontecendo entre a superfície barreira e o tanque:
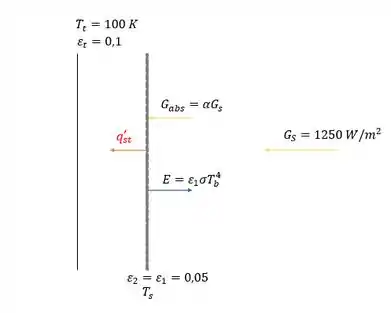
O fluxo térmico tem que ser igual a irradiação que é absorvida pela barreira e a taxa de calor que esta sendo emitida de volta para o espaço, , então podemos escrever esse balanço:
Podemos igualar as duas equações:
Passo 2
Agora temos que isolar e substituir os valores, mas nesse caso vai dar um trabalhinho pra fazer isso, então aqui vai uma dica!!
O que temos é isso daqui:
Agora a gente vai escolher algumas parcelas da equação e trocar por icógnitas que vão deixar mais simples a manipulação!! então ele vai ser nosso :
Isolando:
Substituindo:
Podemos dar mais uma arrumadinha:
Passo 3
Como a barreira é uma superfície cinza e difusa, , lembrando também que , podemos substituir:
Calculando:
Passo 4
Agora podemos calcular :
Substituindo:
Calculando:
Uhuuul!!