Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 103

A absortividade espectral de uma grande superfície difusa é α λ   =   0,9 para λ   <   1   μ m e α λ =   0,3 para λ   ≥   1   μ m . A parte inferior da superfície encontrasse isolada termicamente, enquanto sua parte superior pode estar exposta a uma de duas condições diferentes.

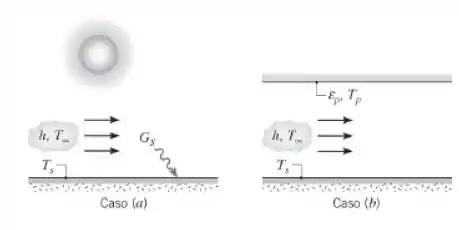
  1. No caso (a), a superfície está exposta ao Sol, que fornece uma irradiação de G S   =   1200 W m 2 , e a um escoamento de ar com T ∞ =   300   K . Se a temperatura superficial é T s = 320   K , qual é o valor do coeficiente convectivo associado ao escoamento do ar?
  2. No caso (b), a superfície está protegida do Sol por uma grande placa e um escoamento de ar é mantido entre essa placa e a superfície. A placa é difusa e cinza, com uma emissividade ε p   =   0,8 . Se v e o coeficiente convectivo é igual ao obtido na parte (a), qual é a temperatura da placa T p necessária para manter a superfície a T s = 320   K ?

Passo 1

É isso ai galerinhaaa !! Vamos continuando?

Bom, antes de qualquer coisa nós vamos fazer o balaço de energia, certo?

No caso (a) nós temos o sol irradiando energia, enquanto temos energia saindo da superfície, q s , e por convecção, q c o n v .

Sendo assim:

q s o l = q s + q c o n v

Substituindo as equações para cada calor:

α S G S = ε s σ T s 4 + h T s - T ∞

Se nós queremos o coeficiente convectivo:

h = α S G S - ε s σ T s 4 T s - T ∞

Vamos ver o que temos?

G S   =   1200 W m 2

T ∞ =   300   K

T s = 320   K

σ = 5,67 × 10 - 8   W m 2 K 4

Como as emissões costumar ocorrem em maiores comprimentos de onda:

ε s = α 2 = 0,3

Nós ainda não temos a absortividade para a superfície, certo?

E para isso nós temos uma relação:

α S = ∫ 0 ∞ α λ E b , λ λ , 5800   K . d λ E b = α 1 F 0 - 1 μ m + α 2 F 1 μ m - ∞

Agora nós vamos olhar lá na Tabela 12.1 e obter que para λ T = 5800   μ m . K , nós temos que:

F 0 - 1 μ m = 0,72

F 1 μ m - ∞ = 0,28

Então:

α S = 0,9 0,72 + 0,3 0,28 = 0,732

Agora é só substituir:

h = 0,732 1200 W m 2 - 0,3 5,67 × 10 - 8   W m 2 K 4 320   K 4 320   K - 300   K

h = 35   W m 2 K

E chegamos ao fim da letra (a) !!

Passo 2

Na letra (b) nós queremos saber qual é a temperatura da placa T p necessária para manter a superfície a T s = 320   K , certo?

Como nós temos neste caso calor entrando por convecção e saindo por radiação:

q r a d = q c o n v

Substituindo:

σ T P 4 - T s 4 1 ε p + 1 ε s - 11 = h T s - T ∞

Substituindo tudo:

5,67 × 10 - 8   W m 2 K 4 T P 4 - 320 4 1 0,8 + 1 0,3 - 11 = 35 320 - 300

T p = 483,665   K

E é isso aí galerinha, chegamos ao fim de mais uma !!

Resposta

  1. h = 35   W m 2 K
  2. T p = 483,665   K
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Problemas 12.20 e 12.25, estimamos a temperatura da superfície da Terra supondo que a Terra fosse negra. A maioria da superfície da Terra é água, que tem uma emissividade hemisférica de ε = 0,96.
Como mostrado na figura, considere o disco A 1 localizado coaxialmente a 1m de distância, porém inclinado 30 ° em relação à reta normal a uma coroa circular A 2 . Qual é a irradiação sobre A 1 devido
Considere os retângulos perpendiculares mostrados na figura.(a) Determine o fator de forma F 12 . (b) Para larguras dos retângulos de X=0,5 ;1,5 e 5m , represente graficamente F 12 como uma função Z b
Considere planos paralelos com extensão normal à página infinita como mostrado na figura. (a) Determine F 12 usando os resultados da Figura 13.4. (b) Determine F 12 usando o primeiro caso da Tabela 13
Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .(a) Det