Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 105
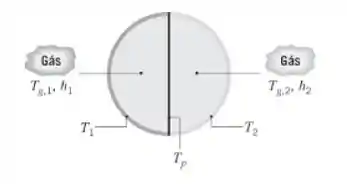
A seção transversal de um longo tubo circular, que está dividido em dois dutos semicilíndricos por uma fina parede, é mostrada na figura. Os lados 1 e 2 são mantidos a temperaturas T1 = 600 K e T2 = 400 K, respectivamente, enquanto as temperaturas médias dos gases que escoam
através dos dutos 1 e 2 são Tg,1 = 571 K e Tg,2 = 449 K, respectivamente. As temperaturas citadas não variam na direção axial. Os gases proporcionam coeficientes de transferência de calor por convecção de , enquanto todas as superfícies dos dutos podem ser aproximadas por corpos negros (ε1 = ε2 = εp = 1). Qual é a temperatura da parede divisória do duto, Tp? Efetuando um balanço de energia no gás no lado 1, verifique se o valor de Tg,1 é de fato igual a 571 K.
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, antes de qualquer coisa, o problema nos pediu duas coisas, a primeira é descobrir a temperatura da parede divisória do duto, Tp, tranquilinho?
Vamos fazer o balaço de energia, certo? Como temos energia saindo por radiação e convecção de 1 e indo para 2:
Substituindo as equações para cada calor:
É muito importante nós lembrarmos aqui da relação:
Então:
Sabemos que:
Então:
Passo 2
A próxima pergunta da questão é confirmar se o valor de Tg,1 é de fato igual a 571 K.
Quando fazemos o balanço para o lado 1 concluímos que o calor convectivo entre o gás e parede deve ser a igual ao gás - superfície:
Para a área:
Então:
Substituindo:
Comprovamos o queríamos !!
E chegamos ao fim de mais umaaa !!