Icebergs podem ser levados a velocidades significativas pelo vento. Admita que o iceberg seja idealizado como um grande cilindro achatado, D = L, com um oitavo de seu tamanho exposto, como na Figura P7.101. Admita que a água do mar esteja em repouso. Se as forças de arrasto superior e inferior dependem das velocidades relativas entre o iceberg e o fluido, deduza uma expressão aproximada para a velocidade permanente do iceberg, V, quando levado pela velocidade do vento U.

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

Nessa questão, temos que deduzir uma expressão para a velocidade de um iceberg que tem um oitavo de seu tamanho emerso em ar. O iceberg pode ser entendido como um cilindro achatado com .

Vamos dar uma olhada no esquema abaixo:

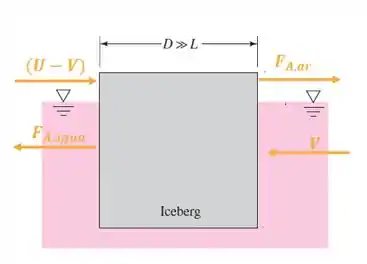
Temos então, uma velocidade da corrente de água vinda da parte frontal e uma velocidade relativa do ar vinda da parte de trás do iceberg.

Se a gente considerar o sistema sem aceleração, as forças de arrasto serão iguais:

Dividindo toda a equação por , teremos:

Desenvolvendo o produto notável:

Chamando e organizando a equação:

Resolvendo a equação quadrática, vamos chegar a:

Pronto, matamos a questão juntos!