Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 37
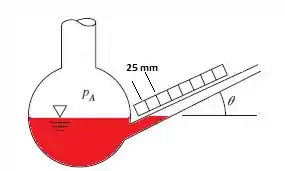
O manômetro inclinado abaixo contém óleo manométrico vermelho Meriam, d = 0,827. Considere que o reservatório seja muito grande. Se o braço inclinado tiver graduações a cada 25 mm, qual deve ser o ângulo se cada graduação corresponde a 48 Pa de pressão manométrica para pA?
Passo 1
Primeiro de tudo vamos transformar essa densidade relativa em absoluta, beleza?
Vamos chamar as graduações de e note que ele já deu pra gente a pressão manométrica (48 Pa), uma vez que podemos ver pelo desenho que há apenas uma graduação completa no tubo inclinado.
Passo 2
Vamos aplicar a hidrostática nesse caso! Se liga como!!
Onde é a altura vertical do tubo inclinado que pode ser dado pela seguinte equação trigonométrica:
Onde a pressão manométrica é dada pela graduação de 48 Pa.
Ao substituir tais valores, encontramos que