Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 79

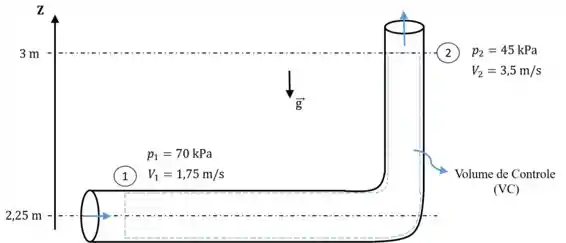
Medidas foram feitas para a configuração de escoamento mostrada na Fig. 8.12. Na entrada, seção 1 , a pressão é 70 kPa (manométrica), a velocidade média é 1,75 m/s e a elevação é 2,25 m. Na saída, seção 2 , a pressão, a velocidade média e a elevação são, respectivamente, 45 kPa (manométrica), 3,5 m/s e 3 m, respectivamente. Calcule a perda de carga em metros. Converta para unidades de energia por unidade de massa.

Passo 1

Considerando a Figura a seguir, este problema buscará obter a perda de carga ao longo do escoamento ilustrado.

Para o cálculo da perda de carga será utilizada a Equação de Energia aplicada entre as seções 1 e 2, conforme expressão:

p 1 ρ 1 g + α V 1 2 2 g + z 1 = p 2 ρ 2 g + α V 2 2 2 g + z 2 + H l t

Note que a expressão a ser utilizada fornecerá resultado em carga (metro).

Para a aplicação da equação apresentada, as seguintes hipóteses são necessárias:

- regime permanente ( ∂ / ∂ t = 0 );

- escoamento incompressível ( ρ 1 = ρ 2 ,   ) e de água ( ρ = 1000   k g / m ³ );

- fator de correção α ≈ 1,0 em ambas as seções de avaliação (o problema não especificou tal parâmetro, logo adotaremos o valor de 1, o qual é característico de escoamento turbulento em tubos).

Os parâmetros p 1 , V 1 , z 1 , p 2 , V 2 e z 2 foram fornecidos pelo enunciado, estando presente na ilustração da solução, de forma que será possível a obtenção da perda de carga H l t .

Passo 2

Tendo como objetivo a perda de carga H l t , ela pode ser escrita como:

p 1 ρ 1 g + α V 1 2 2 g + z 1 = p 2 ρ 2 g + α V 2 2 2 g + z 2 + H l t

H l t = p 1 ρ g + α V 1 2 2 g + z 1 - p 2 ρ g - α V 2 2 2 g - z 2

H l t = p 1 - p 2 ρ g + α V 2 2 - V 1 2 2 g + ( z 1 - z 2 )

Passo 3

Utilizando os parâmetros numéricos conhecidos, a perda de carga é obtida:

H l t = 70 × 10 3 - 45 × 10 3 1000 × 9,81 + 1 × 1,75 2 - 3,5 2 2 × 9,81 + ( 2,25 - 3,0 )

Assim, a perda de carga do escoamento é de:

H l t = 1,33   m

Passo 4

A perda de carga foi obtida em metros, para que tal parâmetro seja descrito em unidade de energia por massa ( J / k g ), deve-se lembrar que:

h l t = g × H l t

Note que h l t representa a perda de energia do escoamento, mas em unidade de energia por massa.

Então, a perda de energia na forma J / k g é de:

h l t = 9,81 × 1,33

h l t = 13,05   J / k g  

Resposta

H l t = 1,33   m

h l t = 13,05   J / k g  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o perfil empírico de velocidade de “lei de potência” para escoamento turbulento em tubo, Eq. 8.22. Para n=7 , determine o valor de r / R para o qual u é igual à velocidade média. Trace um gr
Considere o escoamento laminar completamente desenvolvido de água entre placas paralelas infinitas. A velocidade máxima do escoamento, o espaçamento e a largura das placas são 6,1m / s , 1,9m m e 38m
Água escoa em um tubo horizontal de área transversal constante; o diâmetro do tubo é 75m m e a velocidade média do escoamento é 5m / s . Na entrada do tubo, a pressão manométrica é 275k P a e a saída
Um coeficiente de quantidade de movimento, β , é definido como:Avalie β para um perfil de velocidade laminar, Eq. 8.14, e para um perfil de velocidade turbulenta de “lei de potência”, Eq. 8.22. Trace
Mostre que o coeficiente de energia cinética, α , para o perfil de velocidade turbulenta da "lei de potência” da Eq. 8.22 é dado pela Eq. 8.27. Trace α como uma função de R e , para R e=1×10 4a1×10 7