Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 45
Uma tubulação de vapor com 0,12 m de diâmetro externo está isolada termicamente por uma camada de silicato de cálcio.
(a) Se o isolante possui uma espessura de 20 mm e as suas superfícies interna e externa são mantidas a Ts,1 = 800 K e Ts,2 = 490 K, respectivamente, qual é a perda de calor por unidade de comprimento (q′) da tubulação?
(b) Desejamos analisar o efeito da espessura do isolante na perda de calor q′ e na temperatura da superfície externa Ts,2, com a temperatura da superfície interna mantida em Ts,1 = 800 K. A superfície externa está exposta a uma corrente de ar (T∞ = 25°C), que mantém um coeficiente de transferência de calor h = 25 W/(m2 · K), e a uma grande vizinhança na qual Tviz = T∞ = 25°C. A emissividade da superfície de silicato de cálcio é de aproximadamente 0,8. Calcule e represente graficamente a distribuição de temperaturas no isolante em função da coordenada radial adimensional, (r – r1)/(r2 – r1), na qual r1 = 0,06 m e r2 é uma variável (0,06
Passo 1
Beleza galerinha, vamos lá! (a) A partir de Eq. 3,32 com Ts,2 = 490 K, a taxa de calor por unidade de comprimento é
Passo 2
(b) Executando uma energia para uma superfície de controle ao redor da superfície externa do isolamento, segue-se que
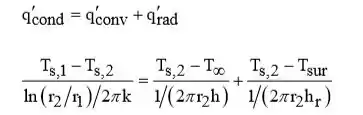
Como mostrado abaixo, a temperatura externa da superfície do isolamento Ts,2 e a perda de calor q′ decaem precipitadamente com aumento da espessura do isolamento a partir dos valores de Ts,2 = Ts,1 = 800 K e q′ = 11.600 W/m, respectivamente, a r2 = r1 (sem isolamento).
