Um satélite esférico com diâmetro D encontra-se em órbita ao redor da Terra e é revestido por um material difuso, que tem absortividade espectral αλ = 0,6 para λ ≤ 3 μm e αλ = 0,3 para λ > 3 μm. Quando o satélite se encontra no lado “escuro” da Terra, ele vê somente a irradiação a partir da superfície da Terra. Essa irradiação pode ser suposta incidindo como raios paralelos e com uma magnitude de GT = 340 W/m2 . No lado “iluminado” da Terra, o satélite vê a irradiação terrestre GT mais a irradiação solar GS = 1368 W/m2 . A distribuição espectral da radiação terrestre pode ser aproximada pela emitida por um corpo negro a 280 K e pode ser admitido que a temperatura do satélite permanece inferior a 500 K.

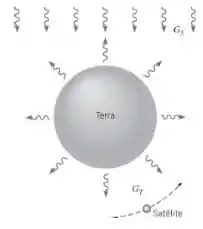
Qual é a temperatura do satélite em condições de regime estacionário quando ele se encontra no lado escuro da Terra e quando ele se encontra no lado iluminado da Terra?

Fala aí! Vamos resolver essa questão aí juntos? Partiu!!

Precisamos encontrar a temperatura do satélite, em duas condições: do lado escuro e do lado iluminado da terra… Humm…

Vamos começar com aquele balanço de energia maroto, ok?

Agora é só isolar nossa temperatura, show!

Mas qual o que vamos usar? Precisamos do , né?

Então vamos ver o seguinte, com de radiação temos um e se a temperatura de , temos então que:

então:

E da mesma forma, com:

Temos: