Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 17

5.17 Deduza a forma diferencial da conservação da massa em coordenadas retangulares por expansão em série de taylor em torno do ponto O dos produtos da massa específica pelas componentes da velocidade: ρ u , ρ v e ρ w . Mostre que o resultado é idêntico à Eq. 5.1a.

Passo 1

Tomando o seguinte volume de controle

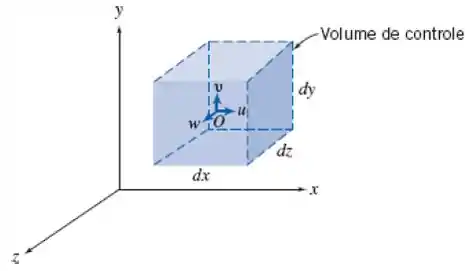
Na direção x, o fluxo de massa pode ser representado por:

m ˙ x = ρ u   d A

m ˙ x = ρ u   d y d z

Na face direita (saindo do VC):

m ˙ x + d x 2 = ρ u + ∂ ρ u ∂ x d x 2 d y d z

Na face esquerda (entrando no VC):

m ˙ x - d x 2 = ρ u + ∂ ρ u ∂ x - d x 2 d y d z

O fluxo na direção x, então vai ser:

m ˙ x = m ˙ x + d x 2 - m ˙ x - d x 2

m ˙ x = ρ u + ∂ ρ u ∂ x d x 2 d y d z - ρ u + ∂ ρ u ∂ x - d x 2 d y d z

m ˙ x = ∂ ρ u ∂ x d x d y d z

Passo 2

De forma bem similar encontramos para direção y e direção z, respectivamente:

m ˙ y = ∂ ρ v ∂ y d x d y d z

m ˙ z = ∂ ρ w ∂ z d x d y d z

A taxa de acúmulo de massa no VC é:

d m d t = ∂ ρ ∂ t d x d y d z

Passo 3

Para ter o fluxo total:

m ˙ x + m ˙ y + m ˙ z + d m d t = 0

∂ ρ u ∂ x d x d y d z + ∂ ρ v ∂ y d x d y d z + ∂ ρ w ∂ z d x d y d z + ∂ ρ ∂ t d x d y d z = 0

Dividindo por d x d y d z :

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z + ∂ ρ ∂ t = 0

Como queríamos demonstrar.

Resposta

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z + ∂ ρ ∂ t = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento tridimensional incompressível?a) u = 2 y 2 + 2 x z ; v = - 2 y z + 6 x 2 y z ; w = 3 x 2 z 2 + x 3 y 4 b) u = x y z
Uma aproximação grosseira para a componente x da velocidade em uma camada-limite laminar e encompressível é uma variação linear de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação cúbica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na b
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação parabólica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
5.21 Para um escoamento incompressível no plano r θ , a componente r da velocidade é dada por V r = - Λ cos ⁡ θ / r 2 . Determine uma possível componente θ da velocidade. Quantas possíveis componentes