Sobre uma determinada faixa de velocidades do ar, , a sustentação, , produzida por um modelo de uma aeronave completa em um túnel de vento, depende da velocidade do ar, da massa específica do ar, , e de um comprimento característico (o comprimento da corda da base da asa, ). Os seguintes dados experimentais foram obtidos para o ar nas condições de atmosfera-padrão:

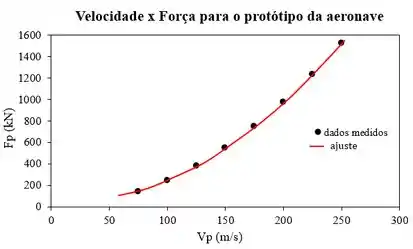
Trace a curva da sustentação em função da velocidade. Usando o Excel, faça uma análise de linha de tendência desta curva e, em seguida, gere e trace um gráfico de dados para a sustentação produzida pelo protótipo, que tem comprimento de corda de 5 m, sobre uma faixa de velocidades de 75 m/s a 250 m/s.

A análise do protótipo pode ser realizada a partir da semelhança dinâmica da força de sustentação, ou seja:

Note que o expoente 1,9954 obtido no Passo 1 pode ser aproximado a 2, de forma que:

De forma de pode ser escrito como:

A relação de velocidade pode ser escrita a partir da semelhança de Reynolds:

Considerando o uso do mesmo fluido no modelo e protótipo:

De forma que:

Então, sabendo a partir do enunciado que e :

Logo, o parâmetro é calculado como:

Assim, o parâmetro pode ser escrito:

Considerando faixa de velocidade de 75 m/s a 250 m/s os valores de são definidos segundo a Tabela abaixo:

Graficamente, pode ser vistou como: