Duas placas em aço inoxidável e ambas com de espessura e com uma de suas superfícies isolada, estão inicialmente a e quando são pressionadas uma contra a outra com o contato feito através das superfícies sem isolamento térmico. Qual é a temperatura da superfície isolada da placa mais quente após o contato?
Passo 1
Aqui nós temos as temperaturas iniciais, propriedades e espessura de duas placas, cada uma isolada em uma superfície. E a partir disso queremos encontrar a temperatura na superfície isolada de uma placa em um tempo prescrito após serem pressionadas juntas. Esquematicamente:
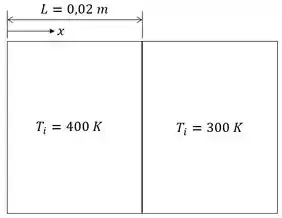
Passo 2
Para resolver essa questão vamos assumir que a condução é unidimensional, as propriedades são constantes e a resistência é desprezível ao contato. No instante em que o contato é feito, as placas se comportam como se fossem semi-infinitas e, como o produto é o mesmo para as duas placas, usamos a equação:
Substituindo os valores encontramos uma temperatura superficial de:
A interface permanecerá nessa temperatura, mesmo após a inserção dos efeitos térmicos nas superfícies isoladas. A resposta transitória da parede quente pode, então, ser calculada a partir de:
Considerando que estamos na condição de a superfície isolada .
Passo 3
Em princípio , e . Temos também que , então e podemos usar a expressão:
E,
Então,