Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 83
Repita o Problema 6.81, considerando que o ar se expande de forma tão rápida que a expansão pode ser considerada como adiabática.
Passo 1
Vamos começar o exercício ilustrando o tanque no momento inicial:
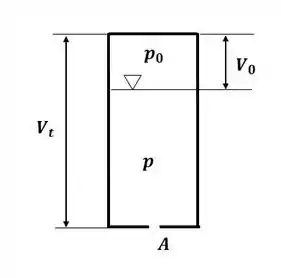
E o tanque em um instante de tempo qualquer:
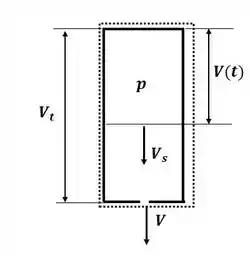
Vamos agora aplicar a equação de Bernoulli entre a superfície do líquido e orifício de saida, então, temos:
Então, nesse caso, sabemos que , pois já iremos encontrar a pressão na forma manométrica. Temos também que e podemos desprezar a diferença entre as cotas e , então a equação se torna:
E a equação da vazão mássica de água é dada por:
Substituindo a expressão encontrada para , temos:
Passo 2
Agora, nós sabemos que a variação de massa de água no tanque pode ser escrita como:
No entanto, sabemos que a variação de volume de ar no tanque corresponde a variação de volume de água, só que enquanto um aumenta, o outro diminui, então podemos escrever:
Agora, como o enunciado nos disse que a expansão do ar pode ser considerada adiabática, temos da equação de estado:
E, como sabemos que a densidade pode ser escrita como:
Substituindo isso na relação anterior:
Só que a massa de ar no tanque não aumenta, o que varia é só seu volume, então temos:
Passo 3
Sabemos que toda a variação de água no tanque sai pelo orifício, então podemos escrever:
Mas, como vimos no passo 2, a variação de volume de água é igual a variação de volume do ar, então, reescrevendo a equação anterior e já substituindo a relação encontrada para , temos:
Agora vamos substituir a relação encontrada para :
Agora vamos separar as variáveis:
Agora integrando a equação dos dois lados:
Resolvendo a integral, temos:
No entanto, nós sabemos que a massa de água pode ser escrita como:
Então, substituindo a expressão encontrada para na equação para a massa de água, temos:
Como temos que o do ar vale 1,4, substituindo esse valor, chegamos em:
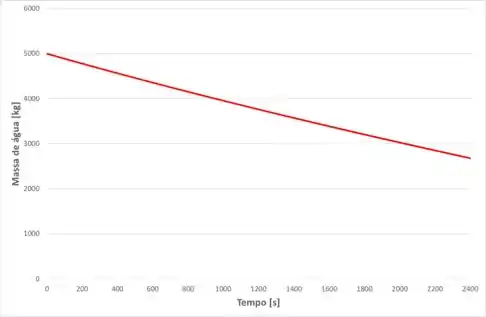
Plotando esse gráfico, temos:
