Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 38

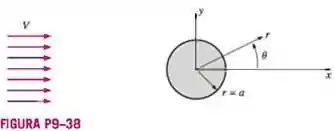
Há muitas ocasiões em que um escoamento livre razoavelmente uniforme de velocidade V na direção x encontra um longo cilindro circular de raio a alinhado normal ao escoamento (Figura P9-38). Exemplos desse tipo incluem o escoamento do ar ao redor de uma antena de automóvel, o vento soprando contra o mastro de uma bandeira ou um poste telefônico, o vento atingindo os fios da rede elétrica, e correntes oceânicas batendo sobre vigas redondas submersas que suportam as plataformas submarinas. Em todos esses casos, o escoamento na parte detrás do cilindro é separado e não permanente e usualmente turbulento. No entanto, o escoamento na metade da frente do cilindro é muito mais permanente e previsível. Na verdade, exceto quanto a uma camada muito fina próximo à superfície do cilindro, o campo de escoamento pode ser aproximado pela seguinte função corrente permanente, bidimensional no plano x y ou plano r θ , com o cilindro centrado na origem: ψ = V ⋅ s e n θ ⋅ r - a 2 / r . Encontre expressões para as componentes da velocidade radial e tangencial.

Passo 1

O problema quer saber as duas componentes da velocidade do fluido no plano bidimensional r θ : a componente radial u r que é a projeção da velocidade do fluido no eixo r e a componente tangencial u θ que é a projeção da velocidade do fluido no eixo θ . A figura abaixo ilustra essas componentes.

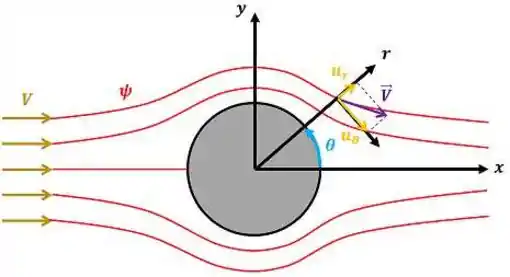
onde V → é a velocidade total do fluido e ψ é a função de corrente associada às linhas de corrente em vermelho. Atenção! Não confunda a função de corrente ψ com a função das linhas de corrente. A função de corrente ψ é uma função que facilita o cálculo das componentes da velocidade do fluido. Já a função da linha de corrente é função que determina a localização dos pontos da linha de corrente (curvas vermelhas).

Além disso, o valor de ψ é constante sobre uma mesma linha de corrente.

No próximo passo nós aprenderemos a calcular as duas componentes da velocidade u r e u θ a partir da função de corrente ψ .

Passo 2

Para calcular as componentes u r e u θ a partir da função de corrente ψ , temos que derivar parcialmente ψ de acordo com as equações 9-27 do livro.

u r = 1 r ⋅ ∂ ψ ∂ θ

u θ = - ∂ ψ ∂ r

Substituindo a função de corrente ψ na fórmula de u r e u θ , encontramos:

u r = 1 r ⋅ ∂ ψ ∂ θ       ⟹       u r = 1 r ⋅ ∂ ∂ θ V ⋅ s e n θ ⋅ r - a 2 r       ⟹       u r = V ⋅ cos ⁡ θ ⋅ 1 - a 2 r 2

u θ = - ∂ ψ ∂ r       ⟹       u θ = - ∂ ∂ r V ⋅ s e n θ ⋅ r - a 2 r       ⟹       u θ = - V ⋅ sen ⁡ θ ⋅ 1 + a 2 r 2

Resposta

u r = V ⋅ cos ⁡ θ ⋅ 1 - a 2 r 2

u θ = - V ⋅ sen ⁡ θ ⋅ 1 + a 2 r 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere novamente o escoamento sobre um corpo de Rankine do Problema 6.122. A meia ­largura, h , do corpo na direção y é dada pela equação transcendente h a = c o t π U h q Avalie a meia ­largura, h
Considere o escoamento representado pela função de corrente ψ = A x 2 y , em que A é uma constante dimensional igual a 2,5m - 1 . s - 1 . A massa específica é 1200 kg/m³. O escoamento é irrotacional?
Determine se a equação de Bernoulli pode ser aplicada entre raios diferentes para os campos de escoamento dos vórtices (a) V → = ω r e → θ e (b) V → = e → θ K / 2 π r .
Considere um escoamento bidimensional: u = a x + b y e v = c x + d y , em que a ,b ,c e d são constantes. Se o escoamento for incompressível e irrotacional, encontre a relação entre a , b , c e d . En
O campo de velocidade para um escoamento bidimensional é V → = A x - B y t i → - ( B x + A y ) j → , em que A = 1s - 2 ,B = 2s - 2 ,t é dado em segundos e as coordenadas são medidas em metros. Este é