Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 123

Considere novamente o escoamento sobre um corpo de Rankine do Problema 6.122. A meia ­largura, h , do corpo na direção y é dada pela equação transcendente

h a = c o t π U h q

Avalie a meia ­largura, h . Determine a velocidade local e a pressão nos pontos ( x , y ) = ( 0 , ± h ) . Considere a massa específica do fluido igual àquela do ar ­padrão.

Passo 1

Bom, o enunciado nos pede para considerar um escoamento da mesmo maneira do problema 6.122, então beleza, já nos dá um norte!

Vamos então lembrar da equação da função de corrente:

ψ = q 2 π θ 1 - q 2 π θ 2 + U r s e n θ

E que tiramos a conclusão que nesse escoamento a função de corrente no ponto de estagnação é:

ψ e s t a g n a ç ã o = 0

O que nos leva a desenvolver o seguinte raciocínio:

ψ = q 2 π θ 1 - θ 2 + U r s e n θ = 0

q 2 π θ 1 - θ 2 = - U r s e n θ

r = q 2 π θ 2 - θ 1 U s e n θ

Relaxa aí! Vamos ao próximo passo!

Passo 2

Vamos então avaliar a equação dada...Trabalhando com θ = π 2 , onde r = h e considerando θ 2 = π - θ 1 ,baseado na imagem que desenhamos aqui em baixo, vamos ter o seguinte:

r = h = q 2 π ( π - θ 1 ) - θ 1 U s e n ( π 2 )

r = h = q 2 π π - 2 θ 1 U

h U = q 2 π π - 2 θ 1

h U = q 2 - q θ 1 π

h U - q 2 π q = - θ 1

π U h q - π 2 = - θ 1

θ 1 = π 2 - π U h q

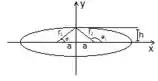
Se a gente tem h = a * t a n θ 1 , temos:

h a = t a n π 2 - π U h q = c o t π U h q

Pegando do exercício anterior, a = 0,3   m , U = 20 m / s e q = 3 π m 2 / s :

h 0,3 = c o t π 20 h 3 π

h 0,3 = c o t 20 h 3

h = 0,1615   m

Passo 3

Show! Já avaliamos a meia ­largura, h . Agora partiu encontrar a velocidade e a pressão nos pontos ( x , y ) = ( 0 , ± h ) :

V _ = q 2 π c o s θ 1 r 1 - c o s θ 2 r 2 + U i ^ + q 2 π s e n θ 1 r 1 - s e n θ 2 r 2 j ^

Fazendo as seguintes considerações: r 1 = r 2 , θ 2 = π - θ 1 → s e n θ 1 = s e n θ 2 , c o s θ 2 = - c o s θ 1

V _ = q c o s θ 1 r 1 + U i ^

Vimos no passo anterior que:

θ 1 = t a n - 1 h a

θ 1 = t a n - 1 0,1615 0,3

θ 1 = 28,5 °

r 1 = 0,3 2 + 0,1615 2

r 1 = 0,341 m

V _ = 3 π c o s 25,3 ° 0,341 + 20 i ^

V _ = 44,3   i ^   m / s

Passo 4

Nossa Saideira agora! Uhull!

Pra achar a pressão vamos usar a equação de Bernoulli:

P 1 ρ + V 1 2 2 + g z 1 = P 2 ρ + V 2 2 2 + g z 2

P ∞ ρ + V 1 2 2 = P ρ + V 2 2 2

P - P ∞ = ρ 2 ( U 2 - V 2 )

P - P ∞ = 1,225 2 ( 20 - 44,3 2 )

P - P ∞ = - 957   N / m 2

Resposta

Meia altura: h = 0,1615   m

Velocidade local: V _ = 44,3   i ^   m / s

Pressão: P = - 957   N / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Aproximamos o escoamento do ar para dentro do acessório de piso, de um aspirador de pó por uma função corrente ψ = - V ˙ 2 π L arctan ⁡ sen ⁡ 2 θ cos ⁡ 2 θ + b 2 / r 2 no plano central (o plano x y )
Bob usará um programa de dinâmica de fluidos computacional para modelar o escoamento permanente de um fluido incompressível através de uma contração brusca bidimensional, conforme mostra a Figura P9-1
Água flui através de um tubo inclinado, longo e reto, de diâmetro D e comprimento L (Figura P9-112).Não há nenhum gradiente de pressão entre os pontos 1 e 2 ;em outras palavras, a água flui através do
Considere o seguinte campo de velocidade permanente, tridimensional em coordenadas cartesianas: V → = u ,v ,w = a x z 2 - b y i → + c x y z j →+ d z 3 + e x z 2 k → onde a , b , c , d e e são constant
O escoamento se separa em um canto agudo ao longo de uma parede e forma uma bolha de separação recirculante conforme mostra a Figura P9-59 (são mostradas as linhas de corrente). O valore da função cor