Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 68

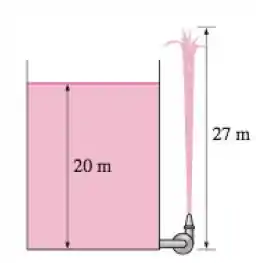
O nível da água em um tanque é de acima do solo. Uma mangueira está conectada à parte inferior do tanque, e o bocal no final da mangueira aponta diretamente para cima. O tanque está no nível do mar e a superfície da água é aberta para a atmosfera. Na tubulação que vai do tanque até o bocal há uma bomba que aumenta a pressão da água. Se o jato de água subir até uma altura de do solo, determine a elevação mínima de pressão fornecida pela bomba para tubulação d’água.

Passo 1

Temos um tanque conectado a uma bomba que jorra água, temos que determinar a pressão mínima para que a coluna de água alcance a altura medida.

Assumindo que o fluxo é constate e incompressível. Assumindo que o atrito entre a água e o ar, atrito do tanque e a água são insignificantes. A superfície da água que está no tanque está aberta a atmosfera.

Para determinarmos a pressão mínima para tal coluna, precisamos determinar dois pontos de referência de nível. Adotarei o topo da superfície do tanque de água como ponto 1, coordenada , e o topo da coluna de água, jorrada pela bomba, como ponto 2, coordenada , com isto temos um .

Para ilustra melhor estes pontos:

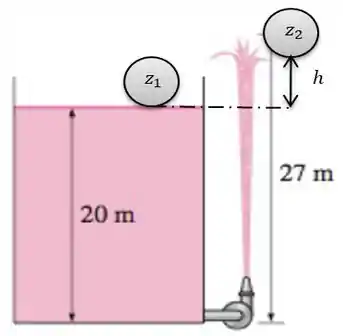
Tendo a densidade padrão da água como

Passo 2

Aplicando a lei de pascal temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

The very large water tank in Fig. P3.147 is dischargingthrough a 4-in-diameter pipe. The pump is running, with aperformance curve hp ft3/s. Estimate the discharge fl ow rate in ft3/s if the pipefricti

For the water channel fl ow of Fig. P3.141, h1 5 0.45 ft,H 5 2.2 ft, and V1 5 16 ft/s. Neglecting losses and assuming uniform flow at sections 1 and 2, fi nd the downstreamdepth h2; show that two real

A water stream flows past a small circular cylinder at23 ft/s, approaching the cylinder at 3000 lbf/ft2. Measurements at low (laminar flow) Reynolds numbers indicate amaximum surface velocity 60 perce

A typical pump has a head that, for a given shaft rotationrate, varies with the fl ow rate, resulting in a pump performance curve as in Fig. P3.181. Suppose that this pump is75 percent efficient and i

For the sluice gate fl ow of Example 3.10, use Bernoulli’sequation, along the surface, to estimate the fl ow rate Q as afunction of the two water depths. Assume constant width b.