Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 51
O núcleo de um reator nuclear de alta temperatura, resfriado a gás, tem tubos de resfriamento com de diâmetro e de comprimento. Hélio entra no sistema a e sai a , quando sua vazão é de por tubo.
a) Determine a temperatura uniforme na superfície do tubo nessas condições.
b) Se o gás de resfriamento utilizado for o ar, determine a vazão requerida se a taxa de remoção de calor e a temperatura na superfície do tubo permanecerem as mesmas. Qual é a temperatura de saída do ar?
Passo 1
Letra a)
Começamos o problema calculando a temperatura média:
Sendo:
;
.
Temos:
Pela Tabela A.4 obtemos as seguintes propriedades do hélio sob a temperatura média de :
Pela Tabela A.4 obtemos as seguintes propriedades do ar sob a temperatura média de :
Passo 2
Calculando o número de Reynolds:
Sendo:
;
.
Temos:
Calculando o número de Nusselt:
Calculando o coeficiente de convecção:
Passo 3
Calculando a temperatura de superfície:
Com:
.
Temos:
Passo 4
Letra b)
Calculando a taxa de calor:
Passo 5
Obtendo a vazão mássica de ar:
Substituindo os termos:
Passo 6
Obtendo o número de Reynolds:
Temos:
Passo 7
Obtendo o coeficiente de convecção do ar:
Assim:
Passo 8
Obtendo a temperatura de saída:
Calculando a temperatura de superfície:
Calculando a temperatura de superfície:
Substituindo os dados:
Passo 9
Para encontrarmos a taxa de fluxo e a temperatura de saída utilizaremos um processo de iteração adotando a primeira temperatura de saída como :
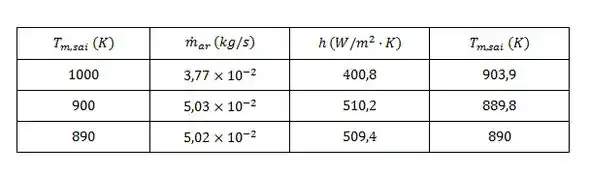
Portanto, a taxa de fluxo é e a temperatura de saída, .