Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 72
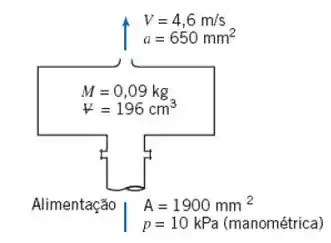
Um objeto, com superfície inferior plana, move-se para baixo com velocidade dentro do jato de líquido do Problema 4.81. Determine a pressão mínima de suprimento necessária para produzir o jato de saída com velocidade . Calcule a pressão máxima exercida pelo jato líquido sobre o objeto plano no instante em que ele etá acima da saída do jato. Estime a força do jato de água sobre o objeto.
Passo 1
Vamos começar ilustrando o exercício adicionando a placa superior e algumas informações fornecidas no enunciado ao desenho de cima (note que o enunciado nos disse que , no entanto, no desenho temos , vamos usar a informação do desenho, pois é mais coerente com o resto dos dados do problema.
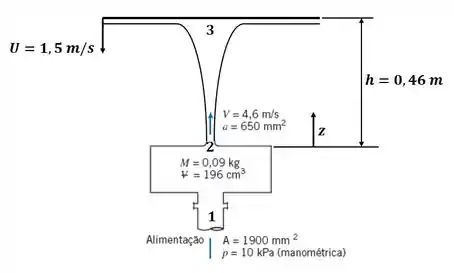
Tá legal, como temos regime permanente e fluxo uniforme entre as seções, podemos aplicar o princípio da continuidade entre os pontos 1 e 2:
Agora vamos aplicar a equação de Bernoulli entre os pontos 1 e 2, dessa forma, temos:
Como o enunciado não nos forneceu nenhuma informação a respeito das cotas e , então podemos desprezar a diferença entre elas. Sabemos também que o ponto 2 descarrega para a atmosfera, então podemos fazer e assim obter a pressão manométrica em , dessa forma, a equação se torna:
Agora vamos substituir a relação encontrada para as velocidades:
Substituindo os valores conhecidos:
Passo 2
Agora vamos calcular a pressão máxima exercida pelo jato líquido sobre o objeto plano no instante em que ele etá acima da saída do jato. Nós sabemos que a pressão máxima é a pressão de estagnação, que é dada por:
Onde, nesse caso, é a velocidade com que o jato chega na placa com relação à própria placa. Para encontra-la, vamos aplicar a equação de Bernoulli entre os pontos 2 e 3, dessa forma, temos:
Nesse caso como temos pressão ambiente nos pontos 2 e 3, os termos de pressão se cancelam e a equação se torna:
Agora, substituindo os valores conhecidos:
Então a velocidade relativa que precisamos será:
Substituindo os valores conhecidos na equação para a pressão de estagnação:
Nesse caso, como a pressão estática em 3 é a pressão atmosférica, fizemos para encontrar uma pressão manométrica.
Passo 3
Agora para estimar a força do jato de água sobre o objeto vamos aplicar a equação da quantidade de movimento 4.18c para o volume de controle ilustrado abaixo:
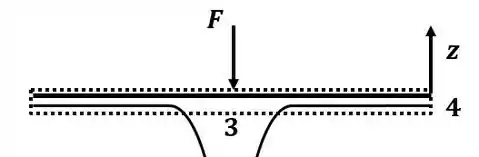
E a equação tem a forma:
No nosso caso, estamos com um regime permanente, então podemos desprezar a primeira integral com a derivada no tempo, vamos desprezar também a ação da força de campo na direção , de modo que . Então a equação se torna:
E, nesse caso, sabemos que que foi encontrado no passo 2, e que pois não é na direção , então a equação se torna:
Como temos continuidade entre os pontos 2 e 3, podemos fazer:
Substituindo os valores conhecidos, temos:
Então, substituindo os valores conhecidos na equação para a força , temos:
Então, como o objeto se move para baixo com velocidade constante, ele está em equilíbrio, dessa forma, a força que o fluido exerce na placa deve ter o mesmo módulo de , só que de sentido oposto, então, como orientamos para baixo, então a força exercida pelo fluido será para cima e de intensidade: