Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 30
Observa-se que a distribuição de temperaturas, em estado estacionário, no interior de uma parede unidimensional com condutividade térmica de e espessura de tem a forma, onde, e está em metros.
(a) Qual a taxa de geração de calor na parede?
(b) Determine os fluxos térmicos nas duas superfícies da parede. De que modo esses fluxos térmicos estão relacionados com a taxa de geração de calor?
Passo 1
Nessa questão nós temos a distribuição de temperatura em uma parede unidimensional com espessura e condutividade térmica definidas. Esquematicamente temos:
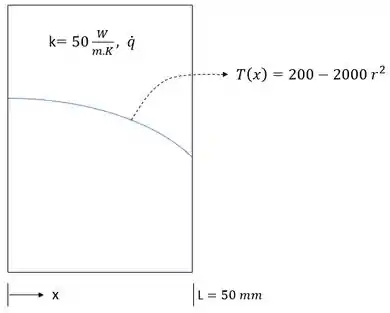
E o enunciado está pedindo pra gente encontrar a taxa de geração de calor, , na parede e os fluxos de calor nas faces da parede e em relação a ou seja, e . Então vamos lá!
Passo 2
Para resolver essa questão, vamos assumir que estamos em condição de estado estacionário, o fluxo de calor é adimensional e as propriedades são constantes.
Resolvendo a letra (a), usaremos a forma apropriada da equação do calor para condições unidimensionais em estado estacionário com propriedades constantes:
Substituindo a distribuição de temperatura na equação acima, temos:
Substituindo os valores,
Passo 3
Já na letra (b), queremos encontrar os fluxos térmicos nas duas superfícies da parede. Para isso, vamos utilizar a Lei de Fourier:
Usando a distribuição de temperatura para analisar o gradiente, temos:
O fluxo para é:
E quando :
Resposta
- e
‘