Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 8.Problemas - Ex. 98
Petróleo bruto na vazão mássica de é aquecido a partir de até através de um trocador de calor de múltiplos tubos. O escoamento do petróleo bruto é dividido por igual entre os tubos do trocador de calor. O diâmetro interno de cada tubo é , e a temperatura na parede interna do tubo é mantida a As propriedades médias do petróleo bruto são: , , , e . Estime a taxa de transferência de calor e o comprimento do tubo.
Passo 1
Podemos desenhe o diagrama esquemático do fluxo do tubo da seguinte maneira:
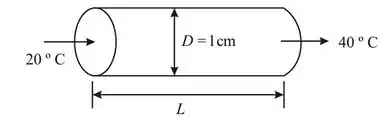
Hipóteses
1) Existem condições de fluxo estáveis.
2) A temperatura da superfície é constante e uniforme.
3) As superfícies internas dos tubos são lisas.
4) A transferência de calor para os arredores é insignificante.
Passo 2
Dados fornecidos:
Diâmetro do tubo:
Comprimento do tubo:
Temperatura de entrada do hidrocarboneto:
Temperatura de saída do hidrocarboneto:
Temperatura da parede do tubo:
Taxa de fluxo de massa:
Número de tubos:
As propriedades médias do hidrocarboneto líquido:
Passo 3
Para resolver essa questão, podemos começar calculando a taxa de transferência de calor usando a seguinte expressão:
Aqui, é a vazão mássica total do petróleo bruto, é o calor específico do petróleo bruto, é a temperatura de saída e é a temperatura de entrada do petróleo bruto. Substituindo os termos da equação pelos dados fornecidos, temos:
Portanto, a taxa de transferência de calor é .
Esta é a quantidade total de transferência de calor para o petróleo bruto dos 100 tubos.
Passo 4
Agora vamos calcular a vazão mássica através de cada tubo. Assim temos:
Aqui, é o número de tubos. Substituindo os dados fornecidos na equação, temos:
Vamos agora calcular o número de Reynolds para o fluxo em cada tubo. Podemos fazer isso usando a seguinte relação:
Aqui, é o diâmetro do tubo e é a viscosidade dinâmica do petróleo bruto. Substituindo os termos da equação pelos dados fornecidos, temos:
Como Reynolds é maior do que , o fluxo é turbulento.
Vamos calcular também o Número de Prandtl. Podemos fazer isso usando a seguinte equação:
Aqui, é a condutividade térmica. Substituindo os termos da equação pelos dados fornecidos, temos:
Passo 5
Com o número de Reynolds e Prandtl, podemos calcular o número de Nusselt usando a equação de Dittus - Boelter. Assim temos:
Substituindo os termos da equação pelos dados obtidos, temos:
Agora que temos o número de Nusselt, podemos calcular a transferência de calor por convecção usando a relação para o número de Nusselt. Assim temos:
Aqui, podemos reescrever a equação para obter isolando o coeficiente de transferência de calor.
Substituindo os termos da equação pelos dados obtidos, temos:
Passo 6
Podemos determinar o comprimento do tubo com a expressão para taxa de transferência de calor usando a lei de Newton de resfriamento. Assim temos
Aqui, é a área da superfície de transferência de calor de um tubo , é a temperatura da superfície do tubo e é a temperatura média do petróleo bruto . Substituindo os termos da equação pelos dados obtidos, temos:
Portanto, o comprimento de cada tubo é .