Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 32

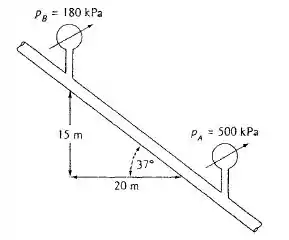
Óleo SAE 30 a 20°C escoa no tubo de 3 cm de diâmetro da figura abaixo que está inclinado a 37°. Para as medidas de pressão mostradas, determine (a) se o escoamento é para cima ou para baixo e (b) a vazão em m³/h.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Vamos pegar as propriedades do nosso fluido, beleza? ρ = 891   k g / m ³ e μ = 0,29   k g / ( m . s )

(a) Bora calcular o valor da altura manométrica em A e da altura manométrica em B!!!

p A ρ g + V A 2 2 g + z A = p B ρ g + V B 2 2 g + z B + h f

Note que temos as velocidades iguais pois estamos dentro do mesmo tubo com mesma seção transversal de escoamento.

Se você observar também, a parcela do lado esquerdo representa a altura manométrica que o ponto B tem, e do lado direito (tirando h f ) representa a altura manométrica de A. Portanto se calcularmos qual altura manométrica for maior, certamente saberemos o sentido do fluxo de óleo.

H G L B = p B ρ g + z b = 180000 891 9,81 + 15 = 35,6   m

H G L A = p A ρ g + z A = 500000 891 9,81 + 0 = 57,2   m

Bem, como a gente esperava né? A pressão em A é bem maior que em B, e agora ao se calcular suas alturas manométricas vemos que realmente, H G L A > H G L B o que indica que nosso fluxo é pra cima!!!

Passo 2

(b) Se a perda de carga é a diferença entre as duas alturas manométricas calculadas

h f = H G L A - H G L B

Vamos considerar um escoamento laminar para podermos abrir nosso valor de perda de carga

h f = 52,7 - 35,6 = 128 μ L Q π ρ g 4 = 128 0,29 25 Q π 891 9,81 0,03 4

Q = 0,000518 m 3 s → 1,86 m 3 h

Bem, vamos checar nosso Reynold pra ver se nossa hipótese foi válida, show?

Passo 3

R e = 4 ρ Q π d μ = 68   L A M I N A R

Show de bola!!! Então nossa suposição de escoamento laminar foi válida e temos que a vazão realmente é de 1,86 m³/h

Resposta

  1. F l u x o   d e   A   p a r a   B
  2. Q = 1,86   m 3 / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um sistema de água é usado em um laboratório para estudar escoamento em um tubo liso. Para atender uma faixa razoável, o número de Reynolds máximo no tubo deve ser 100.000. O sistema é abastecido a pa
Um experimento de bancada consiste em um reservatório com um tubo longo e horizontal de 500 mm de comprimento e diâmetro 7,5 mm ligado em sua base. O tubo sai de um tanque. O escoamento de água a 10°C
Uma piscina pequena é drenada usando uma mangueira de jardim. A mangueira tem 20 mm de diâmetro interno, uma rugosidade absoluta de 0,2 mm e 30 m de comprimento. A extremidade livre da mangueira está
Dados foram obtidos por medições em um trecho vertical de tubo de ferro galvanizado, velho e corroído, com diâmetro interno de 50 mm. Em uma seção a pressão era p1 = 750 kPa (manométrica); em uma segu
Em uma instalação de arcondicionado, é requerida uma vazão de 35 m3/min de ar a 10°C. Um duto de chapa de aço lisa de seção retangular (0,23 m por 0,75 m) é usado. Determine a queda de pressão (em mm