Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 135

Uma piscina pequena é drenada usando uma mangueira de jardim. A mangueira tem 20 mm de diâmetro interno, uma rugosidade absoluta de 0,2 mm e 30 m de comprimento. A extremidade livre da mangueira está localizada 3 m abaixo da elevação do fundo da piscina. A velocidade média na descarga da mangueira é 1,2 m/s. Estime a profundidade da água na piscina. Se o escoamento fosse invíscido, qual seria a velocidade?

Passo 1

Oi pessoal, tudo bem ?

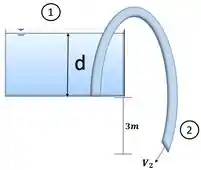
Bem, este é um esboço um pouco mal feito da piscina com a mangueira !!

Para a avaliação da profundidade, diferença de pressão e/ou perda de carga, sempre necessitaremos lembrar da equação da perda de carga:

P 1 ρ ∙ g +   α ∙ V 1 2 2 g + z 1 =   P 2 ρ ∙ g +   α ∙ V 2 2 2 g + z 2   +   h p

Consideremos α = 1 ;

P 2 = P a t m = P 1 ;

Como a piscina é um reservatório, consideramos a velocidade V 1 = 0 ;

Podemos reescrever a diferença z 1 - z 2 = d + 3 .

As perdas de carga serão representadas pela eq da perda de carga maior, e a eq perda de carga menor:

h p = f V ² L 2 g D + K V 2 2 2 g              

K   refere-se ao coeficiente de perda de carga na entrada da mangueira, que recebe o valor de K = 0,5 (Tabela 8.2) .

Podemos admitir também que V 2 = V

Passo 2

Agora, devemos simplificar a equação da energia:

d = V 2 2 g f L D + K + 1 - 3

Da tabela A.7, temos o valor da viscosidade cinemática da água, para a descoberta do Re do problema:

R e = V D υ = 1,2 * 0 , 020 1,01 * 10 - 6                         →                   R e = 2,37 * 10 4

Como

e D = 0,02 20 = 0,010

Podemos encontrar o coeficiente de atrito correspondente na tabela 8.1:

f = 0,04

Passo 3

Podemos então substituir os valores na equação encontrada:

d = 1,2 2 2 * 9,81 0,04 * 30 0,02 + 0,5 + 1 - 3         →       d = 1,51 m

Passo 4

Se o escoamento for invíscido, ou seja, sem atrito, implica dizer que não há perda de carga, então:

h p = f V ² L 2 g D + K V 2 2 2 g = 0            

E:

d = V 2 2 g - 3     → V = 2 g d + 3 = 2 * 9,81 1,51 + 3

Portanto

V = 9,41 m s

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa através de um tubo de 25 mm de diâmetro que subitamente alarga-se para um diâmetro de 50 mm. A vazão através do alargamento é de 1,25 L/s. Calcule o aumento de pressão através do alargament
Um tubo capilar de pequeno diâmetro feito de alumínio trefilado é usado no lugar de uma válvula de expansão em um refrigerador doméstico. O diâmetro interno é 0,5 mm. Calcule a rugosidade relativa cor
Ar na condição padrão escoa através de uma expansão súbita em um duto circular. Os diâmetros do duto a montante e a jusante da expansão são 75 mm e 225 mm, respectivamente. A pressão a jusante é 5 mm
O diagrama de Moody dá o fator de atrito de Darcy, f , em termos do número de Reynolds e da rugosidade relativa. O fator de atrito de Fanning para escoamento em tubo é definido como: f F = τ w 1 2 ρ V
Água escoa através de um tubo de 50 mm de diâmetro que subitamente contrai-se para 25 mm. A queda de pressão através da contração é 3,45 kPa. Determine a vazão volumétrica.