Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas Abrangentes - Ex. 4
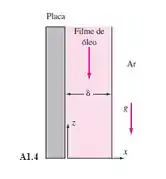
Um óleo de viscosidade e massa específica escoa continuamente para baixo ao longo de uma placa vertical longa e larga, como mostra a Figura A1.4. Na região mostrada, as condições de escoamento estão plenamente desenvolvidas; isto é, a forma do perfil de velocidade e a espessura do filme são independentes da distância z ao longo da placa. A velocidade vertical w torna-se uma função somente de x, e a resistência ao cisalhamento da atmosfera é desprezível.
- Esboce a forma apropriada do perfil da velocidade de w(x), considerando as condições de contorno na parede e na superfície libre do filme.
- Considere que a espessura do filme e a inclinação do perfil de velocidade na parede, sejam medidos por um anemômetro a laser Dopler (a ser discutido no Capítulo 6). Encontre uma expressão para a viscosidade do óleo em função de e da aceleração da gravidade g. Observe que, para o sistema de coordenadas dado, tanto w quanto são negativos.
Passo 1
Bora lá denovooo!
Na (a), vamos esboçar o perfil da velocidade w(x). Note que, perto da placa teremos uma velocidade próxima de zero, ao considerar uma placa imóvel, e assim, ao decorrer para a direita, teremos a velocidade variando com a espessura do filme até , assim:
Não ficou tão bonito, mas o intuito era essa linha vermelha ficar tipo parabólica, mas a questão é, a se afastar da placa, a velocidade aumenta!
Passo 2
Bora pra (b).
O movimento do filme de óleo está para baixo, e temos a viscosidade sendo contrária ao movimento do filme! Num escoamento desenvolvido a força peso irá ser a força de cisalhamento na parede, assim, teremos:
sendo h, a altura do filme.
Essa força peso será igual a força de cisalhamento na parede, assim:
Assim, teremos:
Resposta
Ei, a resposta está no passo a passo :)