Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 15
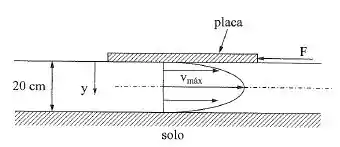
A placa da figura tem uma área de e espessura desprezível. Entre a placa e o solo existe um fluido que escoa, formando um diagrama de velocidades dado por . A viscosidade dinâmica do fluido é e a velocidade máxima do escoamento é . Pede-se:
- O gradiente de velocidades junto ao solo;
- A força necessária para manter a placa em equilíbrio.
Passo 1
Bora lá!! A primeira coisa que a questão pede é o gradiente de velocidade no solo!
O problema dá pra a gente a equação de velocidade:
Se a gente quer o gradiente a gente quer....
Isso mesmo, a derivada!! Então é pra esse caminho que a gente vai!
Multiplicando os termos, fazendo uma distributiva, temos:
Derivando em função de :
O enunciado dá o valor da velocidade máxima
E como queremos esse gradiente no solo, usaremos
E portanto:
Passo 2
A gente quer agora saber quem é a força que deixa a placa em equilibrio, ou seja, parada!!
Se ela esta parada então a força que o fluido faz na placa quando se movimenta deve ser igual a força contraria, que é responsável por deixar ela em equilibrio!!!
Que é:
A área é dada pelo enunciado, , mas precisamos achar :
Para calcularmos a força em que mantém a placa em condição de equilíbrio, realizaremos o calculo do gradiente em , pois a placa está no topo do fluido:
Podemos então encontrar a tensão de cisalhamento relacionada a este gradiente e encontrar a força.
Agora podemos calcular a força: