Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 88

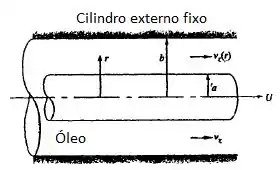
Óleo viscoso da figura abaixo é posto em movimento permanente por um cilindro interno concêntrico movendo-se axialmente à velocidade U dentro de um cilindro externo fixo. Considerando pressão e massa específica constantes e um movimento puramente axial do fluido, resolva a equação (4.38) para distribuição de velocidade do fluido v z ( r ) . Quais são as condições de contorno apropriadas?

Passo 1

Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos? Olha que maneiro!!! O enunciado já disse pra gente qual será a coordenada de interesse para termos o perfil de velocidade, certo? Ele disse pra gente que será a componente z que será função de r.

Em outras palavras temos que v θ = v r = 0 e considerando completamente desenvolvido, temos também que: ∂ ∂ z = 0 . Escoamento permanente e incompressível também é uma hipótese que faremos!!!

Como sempre, vamos apelar primeiro para a equação da continuidade pra ver o que ela vai dizer pra gente de mais possíveis simplificações!!!

∂ ρ ∂ t + 1 r ∂ r ρ v r ∂ r + 1 r ∂ ρ v θ ∂ θ + ∂ ρ v z ∂ z = 0

∂ v θ ∂ θ = 0

Olha, a continuidade também nos deu mais uma simplificação que vamos utilizar na equação de Navier Stokes abaixo!!!

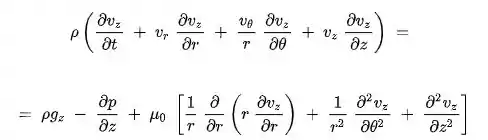
Passo 2

Com nossas simplificações, incluindo aquela que encontramos como resultado da equação da continuidade ao final temos algo do tipo:

μ r d d r r d v z d r = 0

Vamos integrar essa belezinha?

r d v z d r = C 1

∫ d v z = ∫ C 1 r d r  

v z = C 1 ln ⁡ r + C 2

Passo 3

Nossas clássicas condições de contorno são aquelas que sempre usamos! Na parede temos velocidade zero e em “a” vamos ter a velocidade com a velocidade U, correto?

v z a = U         ,               v z b = 0

C 1 = U ln ⁡ a b ,                 C 2 = - C 1 l n ⁡ ( b )

Passo 4

Portanto, nossa solução final nos diz que:

v z = U ln ⁡ r b ln ⁡ a b  

Resposta

v z = U ln ⁡ r b ln ⁡ a b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5.21 Para um escoamento incompressível no plano r θ , a componente r da velocidade é dada por V r = - Λ cos ⁡ θ / r 2 . Determine uma possível componente θ da velocidade. Quantas possíveis componentes
5.15 A componente y da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é v = B x y 3 , em que B = 0,2m - 3s - 1 e x e y são medidos em metros. Encontre a mai
5.19 Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento incompressível?(a) V r = - K / r ; V θ = 0 (b) V r = 0 ; V θ = K / r (c) V r = - K cos ⁡ θ / r 2 ; V θ = - Ks e
5.20 Para um escoamento incompressível no plano r θ , a componente r da velocidade é dada por V r = U cos ⁡ θ .(a) Determine uma possível componente θ da velocidade.(b) Quantas possíveis componentes θ
5.18 Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento incompressível?(a) V r = U cos ⁡ θ ; V θ = - Us e nθ (b) V r = - q / 2 π r ; V θ = K / 2 π r (c) V r = U cos ⁡