Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 5.Problemas - Ex. 15

5.15 A componente y da velocidade em um campo de escoamento em regime permanente e incompressível, no plano x y , é v = B x y 3 , em que B = 0,2   m - 3   s - 1 e x e y são medidos em metros. Encontre a mais simples componente x da velocidade para este campo de escoamento. Determine a equação da linha de corrente para este escoamento. Trace as linhas de corrente que passam pelos pontos (1,4) e (2,4).

Passo 1

Vamos começar pela equação da continuidade e depois simplificando conforme o que ele diz no enunciado:

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z + ∂ ρ ∂ t = 0

Como ele diz que é regime permanentel, admitimos

∂ ρ ∂ t = 0

Ficamos, então, com

∂ ρ u ∂ x + ∂ ρ v ∂ y + ∂ ρ w ∂ z = 0

Como é incompressível, podemos tirar o ρ de dentro da derivada

ρ ∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Simplificando, ficamos com

∂ u ∂ x + ∂ v ∂ y + ∂ w ∂ z = 0

Como é no plano xy, então

∂ w ∂ z = 0

Ficando, finalmente, com

∂ u ∂ x + ∂ v ∂ y = 0

Passo 2

Vamos subtituir

v = B x y 3

Em que B = 0,2   m - 3   s - 1

∂ u ∂ x + ∂ 0,2 x y 3 ∂ y = 0

Resolvendo a derivada em relação a y

∂ u ∂ x + ( 0,2 × 3 ) x y 2 = 0

∂ u ∂ x + 0,6 x y 2 = 0

Arrumando

∂ u ∂ x = - 0,6 x y 2

Separando as variáveis e integrando

d u = - 0,6 x y 2 d x

∫ d u = ∫ - 0,6 x y 2 d x  

u = - 0,6 2 x 2 y 2 + C

u = - 0,3 x 2 y 2 + C

Onde C é uma constante.

Encontramos uma “família de componentes u”, mas a mais simples dela é onde a constante é igual a zero, então nossa resposta fica

u = - 0,3 x 2 y 2

Passo 3

Podemos descrever as linhas de corrente como

d y d x = v u

Substituindo

d y d x = 0,2 x y 3 - 0,3 x 2 y 2

d y d x = - 2 y 3 x  

Separando as variáveis e integrando

3 d y y = - 2 d x x

3 ∫ d y y = - 2 ∫ d x x                         ( i )

3   l n y = - 2   l n x + C

Vamos puxar um pouco os conhecimentos matemáticos sobre log e começar a manipular

3   l n y + 2   l n x = C

l n y 3 + l n x 2 = C

ln ⁡ y 3 x 2 = C

y 3 x 2 = e C

y 3 x 2 = K

Onde K é uma constante.

Ps: A linha de corrente pode ter uma “cara” um pouco diferente, como o y elevado a 3 / 2 , mas continua correto, mudando só a constante. Isso devido a manipulação em (i), podendo ficar 3/2 de um lado, ou 2/3 do outro, ou, até mesmo, da forma que fizemos. Por serem constantes diferentes, vão ser linhas de corrente diferentes, mas ainda assim, linhas de corrente da mesma função.

Passo 4

Para o ponto (1,4)

4 3 × 1 2 = K

K = 64

Então

y 3 x 2 = 64

Isolando o y

y = 64 / x 2 3

Para o ponto (2,4)

4 3 × 2 2 = K

K = 256

Então

y 3 x 2 = 256

Isolando o y

y = 256 / x 2 3

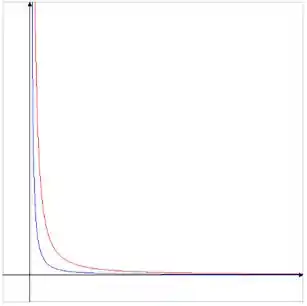
Plotando essas duas funções

Resposta

y 3 x 2 = K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A componente x da velocidade em um campo de escoamento em regime permanente e incompressível no plano x y é v = 2 x y x 2 + y 2 2 Mostre que a expressão mais simples para a componente x da velocidade
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação senoidal de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na
Quais dos seguintes conjuntos de equações representam possíveis casos de escoamento tridimensional incompressível?a) u = 2 y 2 + 2 x z ; v = - 2 y z + 6 x 2 y z ; w = 3 x 2 z 2 + x 3 y 4 b) u = x y z
Uma aproximação grosseira para a componente x da velocidade em uma camada-limite laminar e encompressível é uma variação linear de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U ,
Uma aproximação útil para a componente x da velocidade em uma camada-limite laminar e incompressível é uma variação cúbica de u = 0 na superfície ( y = 0 ) até a velocidade de corrente livre, U , na b