Exercícios de Equação da Continuidade - Lista de Exercícios Resolvida

As coordenadas polares esféricas (r, θ, ϕ) são definidas na figura. As transformações cartesianas são

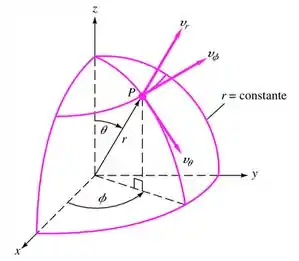
A relação da continuidade cartesiana incompressível (Equação 1) pode ser transformada na forma polar esférica (Equação 2)

Equação 1

Equação 2

Qual é a forma mais geral de quando o escoamento é puramente radial, isto é e são nulas?

Um escoamento idealizado incompressível tem a distribuição tridimensional de velocidade proposta:

Encontre a forma apropriada da função que satisfaz a relação da continuidade

Considere o seguinte campo de velocidade bidimensional para um escoamento permanente e incompressível:

Essa distribuição de velocidade satisfaz a equação da continuidade? Esse escoamento é possível?

Um campo de escoamento incompressível tem os componentes cilíndricos , , , em que C e K são constantes e , . Esse escoamento satisfaz a continuidade? O que ele pode representar fisicamente?

Um pistão comprime gás em um cilindro movendo-se a uma velocidade constante V, como na figura:

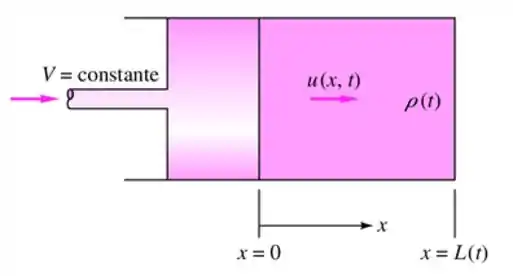
Admita que a massa específica do gás e a posição do pistão em sejam e , respectivamente. Considere que a velocidade do gás varie linearmente de na face do pistão até em . Se a massa específica do gás varia apenas com o tempo, encontre uma expressão para .

Um caso muito comum na mecânica dos fluidos é o caso permanente e incompressível.

Deduza a expressão da Equação da Continuidade para o caso permanente, ou seja, sem variações no tempo, e incompressível, onde é constante.

Uma aproximação razoável para a camada-limite laminar incompressível bidimensional sobre a superfície plana da figura é

Admitindo uma condição de não escorregamento na parede, encontre uma expressão para o componente de velocidade para

Depois encontre o valor máximo de em , para o caso particular do escoamento de ar, quando e .

Um campo de velocidade bidimensional é dado por

Em que K é constante. Esse campo satisfaz a continuidade incompressível? Transforme essas velocidades em componentes polares e . O que esse escoamento pode representar?