Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 11.Problemas Abrangentes - Ex. 6
PA11.6 – Uma turbomáquina interessante [58] é o acoplamento hidrodinâmico da Figura PA11.6, que circula fluido de um rotor de uma bomba primária e faz girar uma turbina secundária em outro eixo separado. Ambos os rotores têm pás radiais. Os acoplamentos são comuns em todos os tipos de transmissões e acionamentos em veículos e em máquinas. O deslizamento do acoplamento é definido como a diferença adimensional entre as rotações dos eixos,
Para um dado volume de fluido, o torque T transmitido é uma função de d, ρ, ωp e do diâmetro D do rotor.
(a) Adimensionalize essa função em dois grupos pi, com um pi proporcional a T.
Testes feitos com um acoplamento de 0,305 m de diâmetro a 2.500 rpm, preenchido com fluido hidráulico de massa específica 897 kg/m3, resultaram nos seguintes dados de torque em função do deslizamento:
(b) Se esse acoplamento operar a 3.600 rpm, com que valor de deslizamento ele transmitirá um torque de 1.220 N.m?
(c) Qual é o diâmetro apropriado para um acoplamento geometricamente semelhante funcionar a 3.000 rpm e 5% de deslizamento e transmitir 813 N.m de torque?
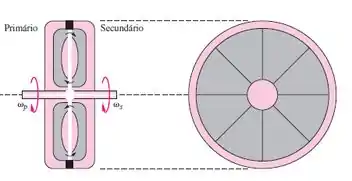
Figura PA11.6
Passo 1
Usando o teorema pi:
-Escrever a função e contabilizar as variáveis:
Veja que são 5 variáveis;
Passo 2
-Listar as dimensões de cada variável:
As dimensões para cada uma dessas variáveis é, pela tabela 5.1 do White, cap. 5, pág. 310
Passo 3
-Determinar valor de j:
Vendo as dimensões de ρ, ωp, e D, vemos que estes não podem formar um grupo adimensional pi, pois entre eles só ρ possui M e ωp possui T, assim j=3. Sendo n o nº de variáveis, então;
Só temos dois grupos adimensionais independentes nesse problema;
Passo 4
-Vamos agora selecionaras variáveis para compor o grupo pi:
Nós podemos pegar exatamente essas três variáveis ρ, ωp, e D, para compor o grupo pi (Π1) proporcional a T
Equacionando os expoentes em um sistema linear:
Comprimento (L)
Massa (M)
Tempo (T)
Pela Eq3 temos que
Pela Eq2
Pela Eq1
Logo,
Passo 5
-O outro grupo pi pode ser referente a variável deslizamento, pois essa já é uma variável adimensional
Passo 6
Vamos agora passar os dados da tabela para a forma adimensional, seguindo a expressão do grupo pi1 encontrado.
Lembrando que as unidades para as dimensões são
Convertendo n para rps
A tabela adimensionalizada é:
Passo 7
(B)
Se n=3600 rpm, para T=1220 N.m
Convertendo n para rps
Assim, pela nova tabela com o torque adimensionalizado
Passo 8
(C)
Se n=3000 rpm, para T=813 N.m...
Convertendo n para rps
Para d=5%, pela tabela adimensionalizada
Assim,
Basta você resolver essa equação para determinar D. Resolve-a
Aplicando os valores
Resposta
A)
B)
C)