Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 51

A comporta AB na figura abaixo tem 1,2 m de comprimento e 0,8 m de largura. Desprezando a pressão atmosférica, calcule a força F na comporta e a posição X de seu centro de pressão.

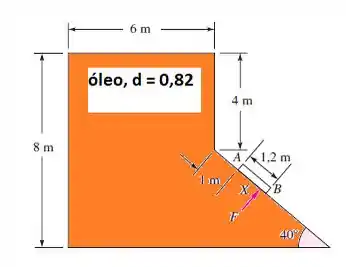
Passo 1

Primeiro de tudo, a gente olha pra esse problema e já viu ali que foi dada a densidade relativa do óleo, então bora já trocar isso pra densidade absoluta do óleo.

ρ ó l e o = d   x   ρ á g u a = 0,82   x   979 = 803   k g / m ³

Vamos pensar agora no seguinte, qual é a profundidade que está essa comporta. Bem, se liga que lá vem trigonometria...

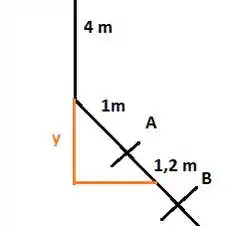
Então a centro de pressão da comporta estará na metade de seu comprimento.

s e n 40 ° = y 1 + 0,6 → y = 1,6   s e n ( 40 ° )

Então, a altura desse centro de pressão é em h = 4 + 1,6   s e n 40 ° = 5,028   m

Passo 2

A gente sabe que pela hidrostática, para uma mesma altura temos a mesma pressão, então se sabemos a profundidade que se encontra o centro de pressão da comporta, sabemos calcular a pressão que atua ali e, portanto, a força de pressão.

P = F A → F p r e s s ã o = P   x   A = ρ ó l e o g h   x   A = 803   x   10   x   5,028   x   1,2   x   0,8 = 38750   N

Passo 3

A linha de atuação da Fpressão pode ser dada pela seguinte fórmula:

y c p = - I X X S e n θ h A

Onde para uma placa plana o produto:

I X X = b L 3 2

Onde b é a largura e L é o comprimento. Portanto, temos:

y c p = - 1 1 2 0.8 1,2 3 s e n 40 ° 5,028   x   1,2   x   0,8 = - 0,0153   m

Ou seja, a posição é dada por X = C e n t r o   d a   p l a c a - y c p = 0,6 - - 0,0153 = 0,615   m

Resposta

F = 38750   N

X = 0,615   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar o módulo e o ponto de aplicação das componentes horizontal e vertical da força exercida pela água sobre a comporta A B da figura, sabendo que sua largura é 0,3m , o raio é 1,8m e a comporta
A comporta A B da figura tem 1,5m de largura e pode girar em torno de A . O tanque à esquerda contém água ( γ = 10.000N / m 3 ) e o da direita, óleo ( γ = 7.500N / m 3 ) . Qual é a força necessária em
Sabendo que γ 1 = 6 γ 2 , calcular a relação x / h para que a comporta permaneça em equilíbrio na posição indicada na figura. Desprezar o peso próprio da comporta.
No esquema da figura, determinar a altura h e a mínima força F para que a comporta A B C permaneça em equilíbrio. Dados: largura = 1,5m ; γ H g = 136000N / m 3 ; γ H 2 O = 10000N / m 3 .
A comporta da figura é rígida e pode girar em torno de B . Sabendo que está em equilíbrio, determinar o comprimento B C .