Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 57

Uma parede composta cilíndrica é constituída por dois materiais com condutividades térmicas k A e k B , que estão separados por um aquecedor elétrico resistivo muito fino. As resistências de contato nas interfaces são desprezíveis.

O líquido bombeado através do tubo se encontra a uma temperatura T ∞ , i e fornece um coeficiente convectivo h i na superfície interna da parede composta. A superfície externa está exposta ao ar ambiente, que se encontra a T ∞ , e e fornece um coeficiente de transferência de calor h e . Em condições de regime estacionário, um fluxo térmico uniforme q q ' ' é dissipado pelo aquecedor.

a) Esboce o circuito térmico equivalente do sistema e represente todas as resistências em termos das variáveis relevantes.

b) Obtenha uma expressão que possa ser usada para determinar a temperatura do aquecedor, T q .

c) Obtenha uma expressão para a razão entre as taxas de transferência de calor para os fluidos externo e interno, q e ' / q i '   Como poderiam ser ajustadas as variáveis do problema para minimizar esta razão?

Passo 1

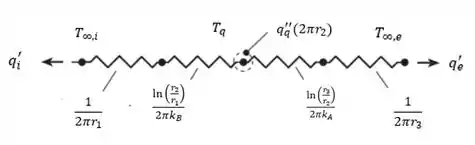
Letra a)

O circuito térmico equivalente do sistema se apresenta como:

Passo 2

Letra b)

Aplicando um balanço de energia, temos que:

E ˙ e n t = E ˙ s a i

Então:

q q ' ' 2 π r 2 = q ' i + q e '

Estendendo:

q q ' ' 2 π r 2 = T q - T ∞ , i 1 h i 2 π r 1 + ln ⁡ r 2 r 1 2 π k B + T q - T ∞ , e 1 h i 2 π r 3 + ln ⁡ r 3 r 2 2 π k A

Simplificando 2 π temos a equação desejada:

q q ' ' r 2 = T q - T ∞ , i 1 h i r 1 + ln ⁡ r 2 r 1 k B + T q - T ∞ , e 1 h i r 3 + ln ⁡ r 3 r 2 k A

Passo 3

Letra c)

Da expressão:

q e ' q i '

Estendendo, temos:

q e ' q i ' = T q - T ∞ , e 1 h i 2 π r 3 + ln ⁡ r 3 r 2 2 π k A T q - T ∞ , i 1 h i 2 π r 1 + ln ⁡ r 2 r 1 2 π k B

Organizando:

q e ' q i ' = T q - T ∞ , e 1 h i 2 π r 3 + ln ⁡ r 3 r 2 2 π k A ⋅ 1 h i 2 π r 1 + ln ⁡ r 2 r 1 2 π k B T q - T ∞ , i

q e ' q i ' = T q - T ∞ , e T q - T ∞ , i ⋅ 1 h i 2 π r 1 + ln ⁡ r 2 r 1 2 π k B 1 h i 2 π r 3 + ln ⁡ r 3 r 2 2 π k A

Simplificando:

q e ' q i ' = T q - T ∞ , e T q - T ∞ , i ⋅ 1 h i r 1 + ln ⁡ r 2 r 1 k B 1 h i r 3 + ln ⁡ r 3 r 2 k A

Resposta

q q ' ' r 2 = T q - T ∞ , i 1 h i r 1 + ln ⁡ r 2 r 1 k B + T q - T ∞ , 0 1 h i r 3 + ln ⁡ r 3 r 2 k A

q e ' q i ' = T q - T ∞ , e T q - T ∞ , i ⋅ 1 h i r 1 + ln ⁡ r 2 r 1 k B 1 h i r 3 + ln ⁡ r 3 r 2 k A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma longa haste cilíndrica de diâmetro de 240m m com condutividade térmica de 0,6W / m ⋅ K experimenta geração de calor volumétrico uniforme de 24.000W / m 3 . A haste é encapsulada por uma luva circu
O vapor pressurizado a 400K flui através de um tubo longo de parede fina de 0,6m de diâmetro. O tubo é envolvido por uma caixa de concreto de seção transversal quadrada e 1,75m de lado. O eixo do tubo
Água quente a 80 ℃ ℃ flui através de um tubo de cobre de parede fina de 30m m de diâmetro. O tubo é envolvido por um invólucro cilíndrico excêntrico que é mantido a 35 ℃ ℃ e tem um diâmetro de 120m m
61 – Nitrogênio líquido (T=77 K) é estocado em um recipiente esférico de parede fina, que é coberto com uma camada de isolamento uniformemente espessa de condutividade térmica k=0,15 W/m.K. A temperat
29 – Um cilindro de diâmetro D=10 mm e temperatura T1=100°C está localizado centralmente em um revestimento quadrado estrudado de baquelite de dimensão w=11 mm. A temperatura ambiente é Ta=25°C e um c