Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 28
Em um elemento combustível cilíndrico para reator nuclear, com de diâmetro, há geração interna de calor a uma taxa uniforme de. Em condições de regime estacionário, a distribuição de temperaturas no seu interior tem a forma, na qual está em graus Celsius e r em metros, enquanto e. As propriedades do elemento combustível são e
(a) Qual é a taxa de transferência de calor, por unidade de comprimento do elemento, em (a linha central do elemento) e em (a superfície)?
(b) Se o nível de potência do reator for subitamente aumentado para, qual são as taxas iniciais da variação de temperaturas com o tempo em e?
Passo 1
Ora ora, o que temos aqui?? Uma questão sobre distribuição de temperatura em estado estacionário em uma haste cilíndrica com geração de calor uniforme de . Ilustrando esse problema:
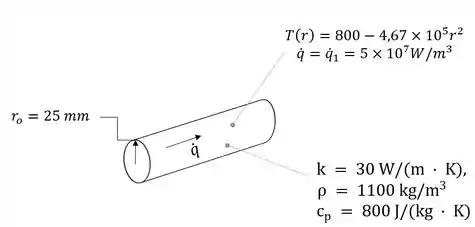
Nós queremos encontrar as taxas de transferência de calor da linha central e da superfície em estado estacionário por unidade de comprimento,. E a taxa inicial de variação da temperatura da linha central e da superfície em resposta a uma mudança na taxa de geração de para
Passo 2
Para resolver essa questão, nós vamos assumir que a condução é unidimensional em , a geração é uniforme e estamos em condição de estado estacionário para .
Começando pela letra (a), para calcular a taxa de transferência de calor, por unidade de comprimento do elemento com diferentes raios. Vamos utilizar a equação da taxa para coordenadas cilíndricas:
e
Então,
Ou,
Onde pode ser pela distribuição de temperatura, Em o gradiente é:
Então,
Em o gradiente de temperatura é:
Ou:
Então, a taxa de calor na superfície externa por unidade de comprimento é:
Passo 3
Já a letra (b) nos pede para calcular as taxas iniciais da variação de temperaturas com o tempo. Essas condições transientes (dependentes do tempo) existirão quando a geração for alterada e, para as suposições prescritas, a temperatura é determinada pela seguinte forma da equação do calor:
Então,
No entanto, inicialmente (em ), a distribuição de temperatura é dada pela forma:
Então,
Então, em toda parede, temos:
Uma parada legal de se observar é que o valor de irá diminuir com o passar do tempo, até que uma nova condição de estado estacionário seja atingida e mais uma vez.
Resposta
- e