Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 2.Problemas - Ex. 23
Em uma parede plana com espessura e condutividade térmica há geração de calor volumétrica uniforme a uma taxa, enquanto transferência de calor por convecção ocorre em suas duas superfícies , cada uma exposta a um fluido com temperatura . Em condições de regime estacionário, a distribuição de temperaturas no interior da parede tem a forma , sendo , , e está em metros. A origem da coordenada encontra-se no plano central da parede.
(a) Esboce a distribuição de temperaturas.
(b) Qual é a taxa volumétrica de geração de calor na parede?
(c) Determine os fluxos térmicos nas superfícies, e . Como esses fluxos estão relacionados com a taxa de geração de calor?
(d) Quais são os coeficientes de transferência de calor por convecção nas superfícies e ?
(e) Obtenha uma expressão para a distribuição de fluxos térmicos, . O fluxo térmico é nulo em algum local?
(f) Se a fonte da geração térmica for subitamente desativada , qual é a taxa de variação da energia acumulada na parede neste instante?
(g) Com , qual temperatura a parede atingirá após um longo período de tempo? Que quantidade de energia tem que ser removida da parede pelo fluido, por unidade de área da parede , para ela atingir esse estado? A massa específica e o calor específico do material da parede são e , respectivamente.
Passo 1
Me acompanha na resolução dessa questão!
Fica de olho para não se perder!
Letra a)
Começamos a questão esboçando a distribuição de temperaturas:
Substituindo os parâmetros dados:
Plotando um gráfico para essa distribuição:
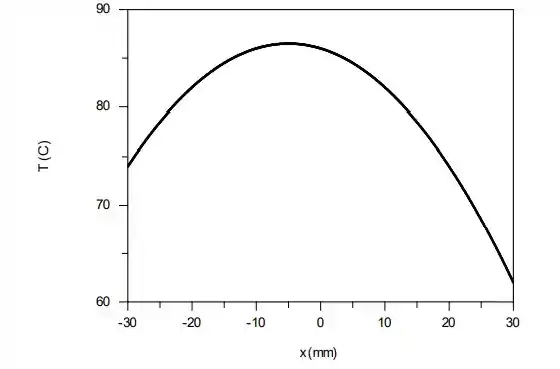
Percebemos:
- Trajetória Parabólica;
- O máximo não ocorre no plano médio ;
- O gradiente na superfície é maior do que em .
Passo 2
Letra b)
Calculando a taxa volumétrica de geração de calor na parede:
Substituindo a equação de distribuição de temperatura:
Substituindo os dados:
Passo 3
Letra c)
Determinando os fluxos térmicos nas superfícies:
Substituindo a equação de distribuição de temperatura:
Para :
Do mesmo modo, para :
Esses fluxos estão relacionados com a taxa de geração de calor da seguinte forma:
Passo 4
Letra d)
Determinando os coeficientes de transferência de calor por convecção nas superfícies e .
Para :
Para :
Passo 5
Letra e)
Obtendo uma expressão para a distribuição de fluxos térmicos, .
O fluxo térmico é nulo em algum local?
Vamos conferir!
Passo 6
Letra f)
Calculando a taxa de variação da energia acumulada na parede:
Passo 7
Letra g)
Com , qual temperatura a parede atingirá após um longo período de tempo?
Com , a parede estará em equilíbrio com o fluido, assim, teremos que sua temperatura final será .
Que quantidade de energia tem que ser removida da parede pelo fluido, por unidade de área da parede , para ela atingir esse estado?
Aplicando um balanço de energia em nosso sistema, temos que:
Com:
Temos:
Até a próxima questão!