A parede plana mostrada na figura, com propriedades constantes e sem geração interna de calor, está inicialmente a uma temperatura uniforme . De repente, a superfície em é aquecida por um fluido à temperatura , com um coeficiente de transferência de calor por convecção . A fronteira em encontra-se perfeitamente isolada.
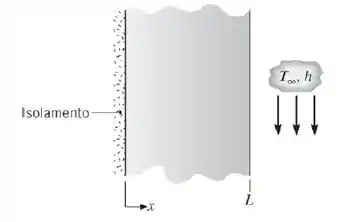
(a) Escreva a equação diferencial e identifique as condições inicial e de contorno que podem ser usadas para determinar a temperatura na parede em função da posição e do tempo.
(b) Em coordenadas , esboce as distribuições de temperaturas para as seguintes condições: condição inicial , condição de regime estacionário , e dois tempos intermediários.
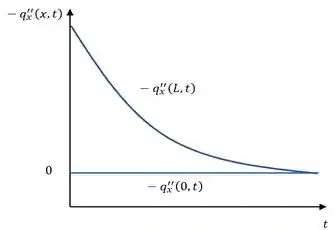
(c) Em coordenadas , esboce o fluxo térmico nas posições e . Ou seja, mostre qualitativamente como e variam com o tempo.
(d) Escreva uma expressão para a quantidade total de energia transferida para a parede por unidade de volume da parede .
Passo 1
Vamos lá! primeiro vamos entender nosso problema, o problema diz que se trata de um sistema unidimensional, logo a troca de calor só ocorre em uma direção, vamos fazer nosso diagrama pra facilitar nossa vida.
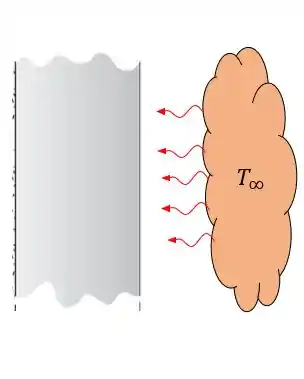
Origem e sentido do aquecimento da parede.
Agora precisamos fazer nossas famosas considerações. Hehe (u.u)
Passo 2
(a)
Tendo tudo isso em mente vamos a nossa letra (a), que nos pede as condições de contorno e a nossa equação diferencial. Para isso vamos escrever nossa lei de Fourier (equação ).
Como nossa condução é unidimensional e não há geração de energia, temos:
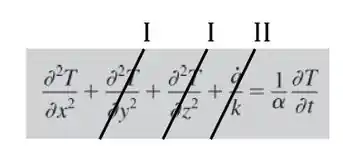
Assim nossa equação fica:
Como quanto nosso fluido aquecedor não aqueceu nossa superfície então a temperatura é , assim nossa equação fica:
Agora pra nossas condições de contorno, na superfície contraria ao aquecedor, não tem fluxo de calor, já que está isolada. Na outra superfície o fluxo de calor vai ser máximo, ou seja:
Passo 3
(b) Bem nosso problema nos pede uma representação gráfica da distribuição de temperatura ao longo da superfície, vamos calcular nossa
Integrando duas vezes em função de e temos:
Como não existe geração de calor e , eventualmente nosso gradiente de temperatura vai se tornar constante.
Assim sendo um aquecimento em duas etapas: (Imagina que ligamos um secador contra a parede deixamos a parede aquecer, então desligamos e religamos rápido o aquecedor e começa novamente o processo).
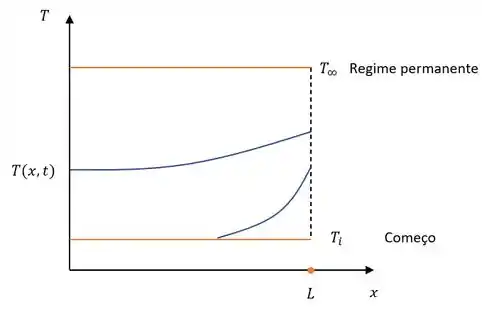
Passo 4
(c) Vamos lá! Nosso problema pede pra escrevermos o fluxo de calor em função do tempo. Temos que lembrar que no regime permanente nosso fluxo vai ser dado por:
Como com o passar do tempo a diferença de temperatura da superfície vai ser igual a temperatura do fluido que tá aquecendo a superfície.
Assim nosso gráfico fica assim.
Passo 5
(d) Estamos terminando! Para escrevermos nossa expressão pra quantidade total de energia transferida temos que integrar nosso fluxo de calor, assim temos:
Sendo a área da superfície vamos dividir ambos os lados pelo volume, que é dado por .
Isso é tudo pessoal! \o/

Resposta
Ei, a resposta está no passo a passo :)