Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 2.Problemas - Ex. 27

Um tanque solar de gradiente salino é um corpo raso de água, composto por três camadas distintas de fluidos, que é usado para coletar energia solar. As camadas externas superior e inferior encontram-se bem misturadas e servem para manter as superfícies superior e inferior da camada intermediária em temperaturas uniformes T 1   e   T 2 ,   o n d e   T 2 > T 1 .Embora exista movimentação do fluido nas camadas misturadas, tal movimento não está presente na camada central. Considere condições nas quais a absorção de radiação solar na camada central implique em geração de calor não-uniforme na forma q = A e - a x e a distribuição de temperaturas nessa camada seja

T x = A k a 2 e - a x + B x + C

As grandezas A ( W / m 3   ) ,   a ( 1 / m ) ,   B ( K / m )   e   C K   são constantes conhecidas que possuem as unidades indicadas, e k é a condutividade térmica, que também é constante.

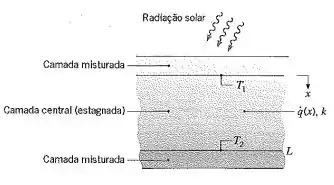
(a) Obtenha expressões para a taxa, por unidade de área, na qual o calor é transferido da camada inferior misturada para a camada central e da camada central para a camada superior misturada.

(b) Determine se as condições do sistema são de regime estacionário ou de regime transiente.

(c) Obtenha uma expressão para a taxa na qual a energia térmica é gerada em toda camada central, por unidade de área superficial.

Passo 1

E ai seres de luz, tudo bem?

Como diz o Homer “Filho, este aparelhinho vai nos ajudar a escapar dessa fria!”

O que sabemos e que a geração de calor não uniforme e distribuição de temperatura na camada central de uma lagoa solar.

Vamos ter que determinar a taxa de calor por unidade de área da camada inferior para a central e da central para a superior na letra A.

Já para a letra B vamos determinar as condições se permanentes ou transitórias.

E finalizando para a letra C vamos expressar a expressão para energia térmica na camada central.

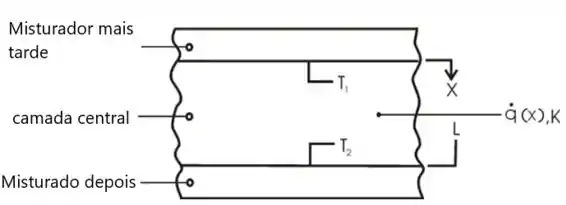
Superposições:

  1. Condução unidimensional
  2. Propriedades constantes

Passo 2

  1. Da lei de Fourier

    2. O fluxo de calor é

    q ˙ = - k ∂ T ∂ x

    q ' ' c o n d ( x = 0 ) = - k ∂ - A k a 2 e - a x + B x + C ∂ x

    = - k A k a + B

    q c o n d ( x = 0 ) ' ' = - k A k a + B  

    q ' ' c o n d ( x = L ) = - k ∂ - A k a 2 e - a x + B x + C ∂ x

    = - k A k a e - a L + B

    q c o n d ( x = L ) ' ' = - k A k a e - a L + B  

    Passo 3

  2. Partindo da equação 2.15

    3. ∂ 2 T ∂ x 2 + q ˙ k = 1 α ∂ T ∂ t

    - A k e - a x + A k e - a x = 1 α ∂ T ∂ t

    ∂ T ∂ t = 0

    Portanto, as condições são estáveis.

    Passo 4

  3. Geração de energia na camada central

E g = A ∫ 0 L q ˙ d x

= A ∫ 0 L e - a x d x

= - A e - a x a x = 0 x = L

E g = A a 1 - e - a L

“Eu não estava mentindo! Estava escrevendo ficção com a boca.”

Resposta

Resposta nos passos

Exercícios de Livros Relacionados

Uma laje de concreto agregado leve de densidade ρ = 1500k g / m 3 consiste em uma matriz sólida de concreto misto de pedra dentro da qual estão pequenas bolsas esféricas de ar. Determine a condutivida
Um cone sólido truncado tem seção transversal circular e seu diâmetro está relacionado à coordenada axial por uma expressão da forma D = a x 3 / 2 , onde a = 2,0m - 1 / 2 .Os lados são bem isolados, e
Considere as distribuições de temperatura associadas a um volume de controle diferencial d x dentro de uma parede plana unidimensional.a) Existem condições de estado estacionário. Energia térmica está
25 – Uma haste composta consiste de dois diferentes materiais, A e B, cada um com comprimento de 0,5L.A condutividade térmica do material A é metade da do material B, isto é, kA/kB=0,5. Esboce a distr
4 – Um disco fino de aço inoxidável de espessura b e raio externo ro foi tratado termicamente a uma temperatura inicial alta e uniforme, Ti. O disco depois é colocado sobre um pequeno suporte para res