Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 13.Problemas - Ex. 37

Considere as cavidades formadas por um cone, um cilindro e uma esfera que têm o mesmo tamanho de abertura ( d ) e dimensão principal ( L ) , como mostrado na figura.

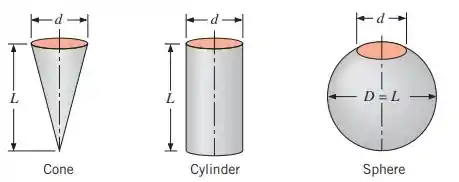
(a) Determine o fator de forma entre a superfície interna de cada cavidade e sua abertura.

(b) Determine a emissividade efetiva de cada cavidade, ε e f , conforme definida no Problema 13.33, admitindo que as paredes internas são difusas e cinzas com uma emissividade ε p .

Passo 1

Opa, tudo bem?Se ajeita aí e vem comigo resolver esse problema!

Letra a)

Começamos o nosso problema aplicando a primeira regra que utilizaremos, a regra da soma, em nossos sistemas:

F 12 + F 11 = 1

Como temos que as superfícies dadas são abertas, elas não podem incidir radiação sobre elas mesmas né?

Assim:

F 11 = 0

Sobrando:

F 12 = 1

Agora, aplicando a regra da reciprocidade:

F 12 = A 2 A 1 F 21

1 = A 2 A 1 F 21

Assim:

F 21 = A 1 A 2

Então, vamos aplicar essa relação para os casos propostos pelo enunciado da nossa questão!

Passo 2

C o n e

Sendo:

A 1 = π d 2 4

A 2 = π d 2 L 2 + d 2 2 1 2

Então:

F 21 = π d 2 4 π d 2 L 2 + d 2 2 1 2

Rearranjando e simplificando:

F 21 = d 2 L 2 + d 2 2 - 1 2

F 21 = 1 2 L d 2 + 1 4 - 1 2

Passo 3

C i l í n d r o

Sendo:

A 1 = π d 2 4

A 2 = π d 2 4 + π D L

Então:

F 21 = π d 2 4 π d 2 4 + π d L

Rearranjando e simplificando:

F 21 = 1 + 4 L d - 1

Passo 4

E s f e r a

Sendo:

A 1 = π d 2 4

A 2 = π D 2 - π d 2 4

Então:

F 21 = π d 2 4 π D 2 - π d 2 4

Rearranjando e simplificando:

F 21 = π d 2 4 π d 2 4 4 D 2 d 2 - 1

F 21 = 1 4 D 2 d 2 - 1

F 21 = 4 D 2 d 2 - 1 - 1

Finalizamos a primeira parte da nossa questão.

Devemos seguir em frente!

Passo 5

Letra b)

Calculando a emissividade efetiva de cada cavidade, ε e f .

Pela relação do Prob. 13.33, temos:

ε e f = q 21 A 2 σ T 1 4

Com:

q 21 = σ T 2 4 - T 1 4 1 - ε 2 ε 2 A 2 + 1 A 2 F 21 + 1 - ε 1 ε 1 A 1

Considerando a superfície como um corpo negro, onde T 1 = 0   K , temos:

q 21 = A 2 σ T 2 4 1 - ε 2 ε 2 + 1 F 21

Voltando a ε e f :

ε e f = A 2 σ T 2 4 1 - ε 2 ε 2 + 1 F 21 A 2 σ T 1 4

Simplificando:

ε e f = 1 F 21 1 - ε 2 ε 2 + 1

Vamos aplicar essa relação para os nossos casos substituindo seu F 21 específico!

Passo 6

C o n e :

ε e f = 1 1 2 L d 2 + 1 4 - 1 2 ⋅ 1 - ε 2 ε 2 + 1

C i l í n d r o :

ε e f = 1 1 + 4 L d - 1 ⋅ 1 - ε 2 ε 2 + 1

E s f e r a :

ε e f = 1 4 D 2 d 2 - 1 - 1 ⋅ 1 - ε 2 ε 2 + 1

Até a próxima questão!

Resposta

a )   C o n e :   F 21 = 1 2 L d 2 + 1 4 - 1 2

C i l í n d r o :   F 21 = 1 + 4 L d - 1

E s f e r a :   F 21 = 4 D 2 d 2 - 1 - 1

b )   C o n e :   ε e f = 1 1 2 L d 2 + 1 4 - 1 2 ⋅ 1 - ε 2 ε 2 + 1

C i l í n d r o :   ε e f = 1 1 + 4 L d - 1 ⋅ 1 - ε 2 ε 2 + 1

E s f e r a :   ε e f = 1 4 D 2 d 2 - 1 - 1 ⋅ 1 - ε 2 ε 2 + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13.50 Uma chapa de alumínio anodizado, com espessura de t = 5 mm, é usada para descartar calor em um dispositivo de potência para uso no espaço. A borda da chapa é fixada à fonte quente e a chapa é ma
13.51 Considere o sistema de descarte de calor em espaçonaves do Problema 13.27, mas sob condições nas quais as superfícies 1 e 2 não podem ser aproximadas por corpos negros.Para superfícies isotérmic
13.54 Oxigênio líquido é armazenado em um vaso esférico com parede delgada e 0,8 m de diâmetro, que encontra-se no interior de um segundo vaso esférico, também com parede delgada e com 1,2 m de diâmet
No fundo de uma grande câmara de vácuo cujas paredes estão a 300 K, um painel negro com 0,1 m de diâmetro é mantido a 77 K. Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesm
Um forno está localizado próximo a um denso conjunto de tubos de transporte de um fluido criogênico. O conjunto de tubos cobertos por gelo formam aproximadamente uma superfície plana com uma temperatu