Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 5.Problemas - Ex. 44
Um avião voa a uma altitude de . Determine a pressão manométrica no ponto de estagnação no nariz do avião se a velocidade for de . Como você solucionaria este problema para uma velocidade de ? Explique.
Passo 1
Bom galera, essa questão é semelhante a alguns exercícios de sonda de Pitot, aqui temos um avião voando a uma certa altura e precisamos determinar a pressão!
Como sabemos o tubo de Pitot pode medir tanto a pressão estática como a de estagnação, e, através da equação de Bernoulli podemos determinar a velocidade. “Mas como???” .
Passo 2
Nós iremos levar em consideração dois pontos, o ponto é distanciado do ponto o qual se localiza na ponta do tubo de Pitot e é usado para medir o ponto de estagnação. Observe:
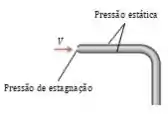
Esse ponto de estagnação é onde o fluido para totalmente, ou seja, e . Substituindo isso na equação do nosso amigo Bernou:
Isolamos a parcela que contém a velocidade da seguinte forma:
A pressão de estagnação é o somatório da pressão estática mais dinâmica, ou seja,
Então, :
Passo 3
A densidade é um valor tabelado, podemos encontra-la na Tabela desse livro! .
Transformamos a velocidade do enunciado
Utilizando a equação do Passo e substituindo os dados do nosso enunciado:
Passo 4
Uma das limitações da equação de Bernoulli é para escoamentos incompressíveis, os quais tem um numero de Mach menor que , ou seja, se a velocidade , portanto dividindo pela velocidade do som:
Assim, essa equação de Bernoulli que utilizamos não pode ser utilizada pois o numero de Mach excedeu o permitido. Mass, pensando no problema criaram uma equação para escoamentos com esse caso, então utilizaríamos ela!!
Prontinho!!
Resposta
; Para esse caso, utilizamos a equação específica de Bernoulli para escoamentos compressíveis.