Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 92
Uma pequena bola de alumínio com D = 2 mm e ρs = 2700 kg/m³ é jogada em um grande recipiente cheio com óleo a 40°C (ρf = 876 kg/m³ e μ = 0,2177 kg/m.s). Espera-se que o número de Reynolds seja abaixo e portanto a lei de Stokes para a força de arrasto, FD = 3πμDV seja aplicável. Mostre que a variação de velocidade com o tempo pode ser expressa como V = (a/b)(1-e-bt) onde a = g(1-ρf/ρs) e b = 18μ/( ρsD²).
Faça um gráfico da variação da velocidade com o tempo e calcule o tempo necessário para que a bola alcance 99 por cento de sua velocidade terminal.
Passo 1
Faaaaaaaaaaaaaala galera, tudo bem? Vem comigo pra gente analisar esse enunciado e resolver esse problema juntos!
Nesse problema a gente tem uma bolinha de alumínio de 2 , que é jogada num tanque com óleo, como demonstra o esquema ilustrativo abaixo:
Mas aí você se pergunta “o que a gente tem que fazer pra resolver essa questão????”.
Bem, nossos objetivos finais são encontrar uma expressão pra velocidade da bolinha ao longo do tempo, fazer um gráfico de velocidade variando ao longo do tempo e, por fim, encontrar o tempo necessário pra velocidade ser 99% da velocidade terminal da bola .
Pra isso, a gente tem que entender que a força resultante nessa queda depende de um balanço de forças entre a força de arrasto , a força peso da bolinha e o empuxo aplicado pelo fluido. Ou seja:
Por isso, a gente tem que utilizar a chamada Lei de Stokes utilizada para quedas de pequenas esferas, dada pela seguinte equação:
Sendo a velocidade de queda da bola.
Além disso, devemos calcular a força peso e o empuxo a partir das equações abaixo:
Sendo a aceleração da gravidade e o volume da esfera lançada no fluido.
Antes da gente ir pros próximos passos, guarde as seguintes propriedades que vamos utilizar nos próximos passos:
Pronto, agora que a gente já analisou esse enunciado e entendemos o que temos que fazer, já podemos partir pra encarar esse problema!
Passo 2
Vamo começar deduzindo uma expressão pra calcular a velocidade da bola ao longo do tempo a partir do balanço de forças que eu te mostrei no Passo 1:
Agora vamos lembrar de um conceito básico da física: a força é uma grandeza que surge quando uma massa é imposta a uma aceleração. Então nossa força resultante pode ser expressa como o produto massa da bolinha e da aceleração dela.
Além disso, a gente tem que lembrar que a aceleração é uma grandeza física que pode ser expressa como a derivada da velocidade com relação ao tempo.
Ou seja, a força resultante pode ser reescrita como:
Substituindo essa expressão no nosso balanço:
Reorganizando a equação:
Lembrando que , vamos chegar à seguinte expressão:
A gente viu no enunciado que podemos agrupar alguns desses termos em e , e portanto:
Note que aqui a gente tem uma EDO separável, que podemos reorganizar na seguinte forma:
Agora, basta que a gente integre os dois lados da equação. Vamos partir da velocidade nula até uma velocidade genérica e do tempo nulo até um tempo genérico :
Passo 3
Agora, vamos fazer um gráfico da variação da velocidade com o tempo.
Primeiro, temos que calcular o parâmetro :
Sendo assim, a expressão pra velocidade em função do tempo pode ser dada pela equação abaixo:
Agora vamos no site Desmos pra plotar essa expressão num gráfico, que está demonstrado na figura abaixo:
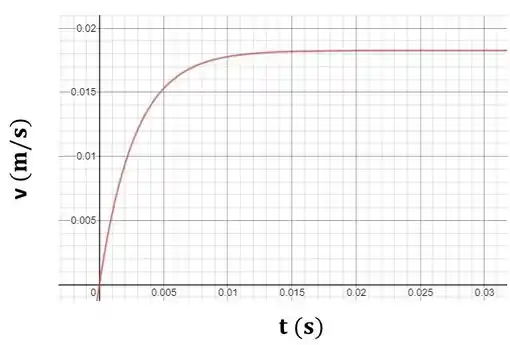
Passo 4
Pra finalizar a questão, vamos calcular o tempo necessário para que a bola alcance 99 por cento de sua velocidade terminal.
Agora, devemos encontrar o valor da velocidade terminal da bolinha.
A gente considera que a velocidade terminal ocorre quando fazemos tender ao infinito. Vamos relembrar a expressão deduzida lá em cima pra velocidade em função do tempo:
Se , então . Logo, a velocidade terminal é:
Agora, vamos deduzir uma expressão pra calcular o tempo a partir da expressão de :
Pra calcular o tempo necessário para que a bola alcance 99 por cento de sua velocidade terminal, a gente faz:
UFA, finalmente finalizamos essa questão juntos!
Resposta
O tempo necessário para que a bola alcance 99 por cento de sua velocidade terminal é .