Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 15

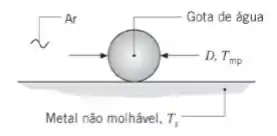
Uma pequena gota de água com diâmetro D = 100   μ m e temperatura T p f = 0 ° C cai sobre uma superfície metálica não molhável que se encontra a T s = – 15 ° C . Determine quanto tempo necessário para a gota congelar completamente. O calor latente de fusão é h s f = 334   k J / k g .

Passo 1

Começamos o problema calculando a temperatura média:

T ¯ = T p f + T s 2

Sendo:

T p f = 0 ° C ;

T s = - 15 ° C .

Temos:

T ¯ = 0 + ( - 15 ) 2 = - 7,5 ° C = 265,5   K

Pela Tabela A.4, “Propriedades termofísicas dos gases à pressão atmosférica “obtemos a condutividade térmica do ar sob a temperatura de 265,5   K por interpolação entre 250   K e 300   K :

k - 22,3 2 6 , 3 - 22,3 = 265,5 - 250 300 - 250

k = 23,5 x 10 - 3   W / ( m ⋅ K )

Pela Tabela A.6, “Propriedades termofísicas da água saturada” obtemos o volume específico de água sob a temperatura de 273   K :

v = 1 x 10 - 3   m 3 / k g

A partir do volume específico, obtemos a densidade:

ρ = 1 v

ρ = 1 10 - 3

ρ = 1000   k g / m 3  

Passo 2

Pela Tabela 4.1 “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados” obtemos o fator de forma para a esfera do Caso 1:

S = 2 π D 1 - D 4 z

Sendo:

z = D 2 ;

D = 100   μ m = 100 x 10 - 6   m .

Temos:

S = 2 π D 1 - 1 2

S = 4 π D

S = 4 π ⋅ 100 x 10 - 6

S = 1,26 x 10 - 3   m

Passo 3

Calculando o volume da gota:

V = π D 3 6

Substituindo D :

V = π ⋅ 100 x 10 - 6 3 6

V = 0,523 x 10 - 12   m 3

Passo 4

Calculando o tempo para a gota congelar completamente:

q c o n d t = ∆ E

S k T p f - T s t = V ρ h p f

Isolando t :

t = V ρ h p f S k T p f - T s

Dados:

V = 0,523 x 10 - 12   m 3 ;

ρ = 1000   k g / m 3 ;

h p f = 334   k J / k g ;

S = 1,26 x 10 - 3   m ;

k = 23,5 x 10 - 3   W / ( m ⋅ K ) ;

T p f = 0 ° C = 273   K ;

T s = - 15 ° C = 2 58   K .

Temos:

t = 0,523 x 10 - 12 ⋅ 1000 ⋅ ( 334 x 10 3 ) 1,26 x 10 - 3 ⋅ 23,5 x 10 - 3 ⋅ 273 - 258

t = 0,394   s

Resposta

t = 0,394   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um pequeno cilindro cujas superfícies superior e inferior são isoladas. O cilindro está inicialmente a uma temperatura uniforme T i , sendo submetido a convecção a partir da superfície later
Um reservatório esférico de aço inoxidável k =15Wm·K de 8 m de diâmetro interno e 1,5 cm de espessura é usado para armazenar água com gelo a 0°C. O reservatório está localizado em uma sala cuja temper
O vapor a 280°C escoa em um tubo de aço inoxidável k =15Wm·K cujos diâmetros interno e externo são de 5 cm e 5,5 cm, respectivamente. O tubo é coberto com isolante de lã de vidro k =0,038Wm·K de 3 cm
Uma seção de 50 m de comprimento de um tubo de vapor cujo diâmetro externo é de 10 cm passa por um espaço aberto a 15°C. A temperatura média da superfície externa do tubo é medida em 150°C. Se o coefi
Reconsidere o Problema 3-73. Usando EES (ou outro programa), trace a parcela do custo da energia da água quente devido à perda de calor do tanque em função da temperatura da água quente na faixa de 40