Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 10
Com base nas taxas de transferência de calor por condução adimensionais para os casos 12–15 na Tabela 4.1, encontre fatores de forma para os seguintes objetos com temperatura , localizados na superfície de um meio semi-infinito que está à temperatura . A superfície do meio semi-infinito é adiabática.
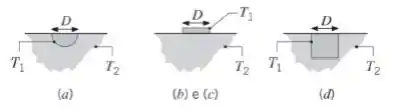
a) Um hemisfério enterrado, com o plano no mesmo nível da superfície.
b) Um disco sobre a superfície. Compare o seu resultado com o da Tabela 4.1, caso 10.
c) Um quadrado na superfície.
d) Um cubo enterrado, com uma face no mesmo nível da superfície.
Passo 1
Expressando a equação da taxa de calor por condução sem dimensão para meio infinito:
Sendo:
;
;
;
;
.
Isolando :
A relação de comprimento característico para meio infinito se dá por:
O fator de forma para meio infinito é:
Substituindo os termos na equação:
Considerando que o meio está sujeito a superfície semi-infinita, temos:
Passo 2
Letra a)
Calculando o fator de forma para o objeto do hemisfério enterrado, com o plano no mesmo nível da superfície.
Obtendo a área ativa e o fator de forma para um hemisfério na Tabela 4.1, “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados – Caso 12”:
A taxa de condução de calor sem dimensão:
Substituindo na equação de fator de forma:
Passo 3
Letra b)
Calculando o fator de forma para um disco sobre a superfície.
Obtendo a área ativa e o fator de forma de um disco na Tabela 4.1, “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados – Caso 13”:
A taxa de condução de calor sem dimensão:
Substituindo na equação de fator de forma:
Passo 4
Letra c)
Calcule o fator de forma para um quadrado na superfície.
Obtendo a área ativa e o fator de forma para um quadrado na Tabela 4.1, “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados – Caso 14”:
A taxa de condução de calor sem dimensão
Sabendo que é o comprimento e é a largura, para um quadrado, temos:
Então:
Substituindo na equação de fator de forma:
Passo 5
Letra d)
Calculando o fator de forma para um cubo enterrado, com uma face no mesmo nível da superfície.
Consideremos que a taxa de altura do objeto inteiro (cubo) seja igual a 2.
Obtendo a área ativa e o fator de forma para um cubo na Tabela 4.1, “Fatores de forma de condução e taxas de calor de condução sem dimensão para sistemas selecionados – Caso 15”:
A taxa de condução de calor sem dimensão:
Substituindo na equação de fator de forma:
O fator de forma para um cubo de igual a 2 é