Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 70

O vapor a 280°C escoa em um tubo de aço inoxidável k =   15   W   m   ·   K cujos diâmetros interno e externo são de 5 cm e 5,5 cm, respectivamente. O tubo é coberto com isolante de lã de vidro k =   0,038   W   m   ·   K de 3 cm de espessura. O calor é perdido para o meio a 5°C por convecção natural e radiação, com coeficiente combinado de transferência de calor por convecção natural e radiação de 22   W   m 2   ·   K . Considerando que o coeficiente de transferência de calor no interior do tubo é de 80   W   m 2   ·   K , determine a taxa de perda de calor do vapor por unidade de comprimento do tubo. Determine também a queda de temperatura através da tubulação e da camada de isolamento.

Passo 1

Shoow!!

Vamos desenhar o que estamos lendo no problema:

Agora que sabemos nós podemos desenhar as resistências:

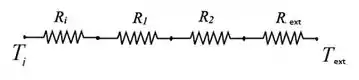
Então nós teremos aqui a resistência a convecção que é interna, segui da resistência oferecida pela camada de aço e pelo isolante. E por último nós teremos a resistência a convecção combinada à radiação externa.

Então:

R   i = 1 h i × A i

R 1 = R c i l i n d r o , a ç o = ln ⁡ r 2 r 1 2 π k a ç o L

R 2 = R c i l i n d r o , i s o l = ln ⁡ r 3 r 2 2 π k i s o l L

R e x t = 1 h e x t × A e x t

Já sabemos como calcular as resistências, só precisamos das áreas.

Bora lá?

Passo 2

A área interna da seção transversal é dada por:

A i = π d i L

A i = π ( 0,05   m ) ( 1   m ) = 0,157   m 2

Para a área externa nós levamos em consideração o diâmetro externo do tubo de aço mais o comprimento do isolante:

d 3 = d e x t = d i + 2 l i s o l a n t e = 5,5   c m + 2 × 3   c m = 11,5   c m

Então:

A e x t = π d 3 L

A e x t = π ( 0,115   m ) ( 1   m ) = 0,3613   m 2

Passo 3

Agora vamos substituir nas fórmulas e achar nossas tão queridas resistências:

R   i = 1 80 W m 2 K × 0,157   m 2 = 0,08 K W

R e x t = 1 22 W m 2 K × 0,3613   m 2 = 0,1258 K W

Sabendo que r = d 2 podemos adaptar as resistências:

R 1 = ln ⁡ d 2 d 1 2 π k a ç o ( 1   m )

R 2 = ln ⁡ d 3 d 2 2 π k i s o l L

Substituindo:

R 1 = ln ⁡ 5,5 5,0 2 π 15 W m K ( 1   m ) = 0,00101 K W

R 2 = ln ⁡ 11,5 5,5 2 π 0,038 W m K ( 1   m ) = 3,089 K W

Como estão todas em séria, a resistência total é dada por:

R T = R i + R 1 + R 2 + R e x t

R T = 0,08 K W + 0,00101 K W + 3,089 K W + 0,1258 K W

R T = 3,2958 K W

Passo 4

Agora sim nós conseguimos saber qual será a perda de calor para o ambiente.

Usamos a fórmula do calor:

Q ˙ = T v a p o r - T p e r d i d a R t o t a l

Substituindo:

Q ˙ = 280 ° C - 5 ° C 3,2958 K W

Como a variação em graus Celsius e kelvin é a mesma:

Q ˙ = 83,439   W

Beleza! Achamos nossa primeira resposta!

Passo 5

A próxima pergunta é: Qual a queda de temperatura através do tubo?

Para responde-la basta usarmos a fórmula anterior para o calor, só que neste caso levaremos em conta somente a resistência do tubo:

Q ˙ = ∆ T t u b o R 1

Isolando a variação:

∆ T t u b o = Q ˙ R 1

E substituindo:

∆ T t u b o = 83,439   W × 0,00101 K W

∆ T t u b o = 0,0835   K

Para o isolamento fazemos a mesma coisa:

∆ T i s o l = Q ˙ R 2

E substituindo:

∆ T i s o l = 83,439   W × 3,089 K W

∆ T i s o l = 257,74   K

E fiiim !!

Resposta

  1. 83,439   W ;
  2. ∆ T t u b o = 0,0835   K | ∆ T i s o l = 257,74   K .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A temperatura de ebulição à pressão atmosférica do nitrogênio ao nível do mar (pressão de 1 atm) é -196°C. Portanto, o nitrogênio é comumente usado em estudos científicos de baixa temperatura. A tempe
Um fio elétrico de 2,2 mm de diâmetro e 14 m de comprimento é enrolado firmemente com uma cobertura plástica de 1 mm de espessura cuja condutividade térmica ék =0,15Wm·K . As medições elétricas indica
Reconsidere o Problema 3-80E. Usando o software EES (ou outro programa), investigue os efeitos da condutividade térmica do material do tubo e do diâmetro externo do tubo no comprimento do tubo necessá
Na indústria farmacêutica, um tubo de cobre k = 400 W m·K com diâmetro interno de 20 mm e espessura de parede de 2,5 mm é usado para transportar oxigênio líquido para um tanque de armazenamento. O oxi
A taxa de transferência de calor da parede de um tubo circular com convecção agindo sobre a superfície externa é dada, por unidade de seu comprimento, q ˙ = 2 π L T i - T o ln ⁡ r o / r i k + 1 r o h