Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 76

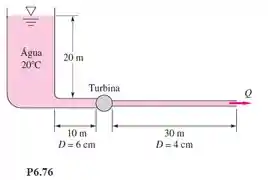
A pequena turbina na Figura P6.76 extrai 400 W de potência do escoamento da água. Ambos os tubos são de ferro forjado. Calcule a vazão Q em m 3 / h . Esboce as LE e LP corretamente.

Passo 1

Bora lá!

Para a água temos, ρ = 998   k g / m 3 e μ = 0,001   k g / ( m ⋅ s ) , aproveitamos também e coletamos o valor da rugosidade relativa do tubo de ferro forjando sendo ϵ D 1 = 0,046 m m 60 m m = 0,000767 e ϵ D 2 = 0,046 m m 40 m m = 0,00115 . Considerando a velocidade na superfície do tanque desprezível e como ambos lados estão abertos para a atmosfera, as pressões irão se cortar, logo, nossa equação de energia ficará da seguinte maneira:

z 1 - z 2 = V 2 2 2 g + h f 2 + h f 1 + h t u r b i n a

Sendo,

h f 1 = f 1 L 1 D 1 V 1 2 2 g

h f 2 = f 2 L 2 D 2 V 2 2 2 g

Assim,

z 1 - z 2 = V 2 2 2 g + f 2 L 2 D 2 V 2 2 2 g + f 1 L 1 D 1 V 1 2 2 g + h t u r b i n a

Tendo,

h t u r b i n a = P ρ g Q = 400   W 998 k g m 3 9,81 m s 2 Q

Logo,

h t u r b i n a = 400   W 998 k g m 3 9,81 m s 2 Q = 20   m - 8 f 1 L 1 Q 2 π 2 g D 1 5 - 8 f 2 L 2 Q 2 π 2 g D 2 5 - 8 Q 2 π 2 g D 2 5

Passo 2

Bora dar um chute na vazão, assim, encontraremos:

Q c h u t e = 0,003 m 3 s → R e 1 = 4 ρ Q π μ D 1 = 63500 → f 1 m o o d y = 0,0226

R e 2 = 95300 → f 2 m o o d y = 0 , , 0228

Mas cara, se analisarmos, esse não é um chute legal. Repare que se substituirmos os valores na equação de energia, teremos que os valores do lado direito e esquerdo da turbina vão divergir!

Porém, se chutarmos um valor de Q = 0,00413   m 3 / s , chegaremos em um h t u r b = 9,9   m , um valor que converge para ambos os lados da turbina, assim, temos nossa vazão:

Q = 0,00413 m 3 s = 15 m 3 h

Resposta

Q = 15   m 3 / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa em regime permanente em um tubo de ferro fundido, horizontal, de 125 mm de diâmetro. O tubo tem comprimento de 150 m e a queda de pressão entre as seções 1 e 2 é 150 kPa. Determine a vazão
Investigue o efeito do comprimento de tubo sobre a vazão, calculando a vazão gerada por uma diferença de pressão, Δp = 100 kPa, aplicada a um comprimento L de um tubo liso de diâmetro D = 25 mm. Trace
Dois tubulões verticais de igual diâmetro, abertos para a atmosfera, estão conectados por um tubo reto conforme mostrado. Água escoa por gravidade de um tubulão para o outro. Para o instante mostrado,
Os alunos da residência universitária estão colocando uma piscina infantil no segundo andar e pretendem enchê-la com água de uma mangueira de jardim. A piscina tem um diâmetro de 1,5 m e uma profundid
Investigue o efeito da rugosidade do tubo sobre a vazão, calculando a vazão gerada por uma diferença de pressão, Δp = 100 kPa, aplicada a um comprimento L = 100 m de um tubo de diâmetro D = 25 mm. Tra